by Nicolas Copernicus
December 15th, 2008
Back in the 1950s, a famous writer referred to De Revolutionibus (the Latin title of this book) as "the book nobody read". There's a good reason why -- which I'll get to soon. But in response to that, Own Gingerich, a professor of astronomy and later professor of the history of science at Harvard, wrote a book in 2004 with the title "The Book Nobody Read", arguing that in fact lots of people read it. He had gone all over the world, examining every single known copy of De Revolutionibus -- some 600 in all -- for annotations, side notes, or other indications that people actually read and understood the book. He discovered that lots of people had read the book over the centuries. However "lots" means different things to different people. What Mr. Gingerich meant was that hundreds of people have read the book in the 450 years since its publication. I think that pretty much proves that "nobody" read the book.
There's a very good reason why nobody read the book: it's long, it's boring, and it's full of tedious calculations that are difficult to follow. Let me show you what I mean: (This is part of a calculation involving the orbit of Mars)
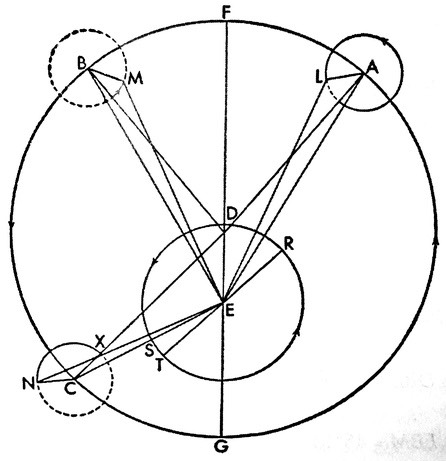
Here's the beginning of the accompanying text: Let eccentric circle ABC be described with center D, and with FDG as the diameter through both apsides; and let E the center of the orbital circle of annual revolution be on the diameter. Let A, B, and C be the points of solar opposition, in that order; and let arc AF = 41º34', arc FB = 40º11', and let arc CG = 44º21'. At the separate points A, B, and C let the epicycle be described with one-third of the distance DE as radius. And let AD, BD, CD, AE, BE, and CE be joined. On the epicycle let AL, BM, and CN be joined, but in such a way that angle DAL = angle ADF and angle DBM = angle BDF.
From this point forward Copernicus begins a series of geometric calculations that culminate in this conclusion:
But at this last observed opposition of Mars the planet was seen at 235º54', being 127º5' distant from the apogee of the eccentric circle, as was shown; therefore the position of the apogee of the eccentric circle of Mars was at 108º50' in the sphere of the fixed stars.
Now, I have a lot of experience with this stuff; I have done some of these calculations myself. I know about planetary orbits and the various means of calculating positions in various coordinate systems. (And in fact, you should know that Copernicus is doing his calculations in the plane of the ecliptic.) Yet, as I march through his calculations, step by bloody step, I get lost. Perhaps it's the use of archaic terminology: I still haven't figured out what he means by the "orbital center of annual revolution" (does he mean the center of the earth's orbit or the center of Mars' orbit?) He talks about multiple points of solar opposition, which happens on different years, but he's not clear WHEN those solar oppositions took place. If I flip back through the pages I'm sure I can find them, but I'm not that obsessive. And it does take a change of mental gears to do all the calculations in the ecliptic coordinate system. After all, the orbit of Mars is inclined slightly to the plane of the ecliptic, yet this calculation does not include that fact.
In all honesty, I must confess that I didn't read this book either. I read most of the words on most of the pages, but a lot of the words just went in one eye and out the other. I was able to follow some of the early calculations, which were fairly simple, but as he dug deeper into his material, I lost patience with the painstaking effort of following his logic.
Nevertheless, this book is immensely important, and it contains special information for me: I am still honing my thesis concerning the development of rational thinking, and this is a revealing snapshot of the state of Western rationalism in the early 16th century.
I was flabbergasted by the mathematical sophistication Copernicus applied to the problem. Four factors in particular knocked my socks off. The first was his use of three-dimensional geometry of spheres. This guy started off with a chapter on spherical trigonometry. What's so surprising about this is that the Greeks never did (as far as I know) any spherical trig. Where did Copernicus pick that up?
The second, even more astounding discovery, was Copernicus' use of trig. Actually, he wasn't using what we call trig; there were no sines, cosines, tangents, or any of those other functions that are part of fully-developed trigonometry. Instead, Copernicus had a more primitive system based on chords of circles. But he knew how to used that system to carry out most of the calculations that can be done with regular trig. I never figured out where he got his trig tables from; I suspect that they are derived from careful calculations, or perhaps from outright measurements. But he had them, and they were good enough to take his calculations down to one minute of arc accuracy -- that's one part in 5,400!
The third shocker was his use of ancient observations to carry out detailed analysis of orbital parameters of the moon, the earth, and the planets. The problems of making that work are daunting; he had to translate between different calendraic systems, different timekeeping systems, and take into account the differences in longitude. In all honesty, I suspect that such transformations cannot be reliable -- yet the audacity of even attempting them is awe-inspiring.
Lastly, the numerical computations that Copernicus carried out are mind-boggling. Remember, this was a bit before we had digital calculators. Everything had to be worked out by hand, using pen and paper. The methodologies for such simple tasks as multiplication and division were still relatively new in his time. The whole idea of multiplying digit-by-digit, carrying tens, shifting the columns -- that stuff wasn't even possible with Roman numerals, and the Arabic (actually, Indian) numerals had started to get broad use in Europe only a hundred and fifty years before Copernicus. The methods for multiplication and division by hand were published by a Venetian in the late 1400's -- and Copernicus was using this new-fangled mathematics at industrial-scale levels just fifty years later. Astounding! I very much doubt that I could have carried out the mountains of calculations that Copernicus did to arrive at his conclusions. (As it happens, Copernicus made a lot of arithmetic mistakes, but they were not serious enough to damage his overall conclusions.)
So how was it that Copernicus' book started the "Copernican Revolution"? In truth, it didn't -- not at first. A hundred years after Copernicus, Galileo was in hot water with the Church for espousing Copernican views. It really wasn't until late in the 17th century that the Copernican hypothesis was broadly accepted. It took the work of Galileo and Newton -- and 150 years -- to overwhelm the opposition to Copernicus.
