Today’s problem is a common one in balancing coupled differential equations. The title springs from its exemplar: a study of the populations of foxes and hares in a Canadian region. In this region, foxes were the primary predator of hares, and hares were the primary prey of foxes. You’d therefore expect their populations to stabilize at some ratio based on the number of hares a fox needs to eat annually. That turned out not to be the case. The populations of the two species oscillated in vaguely sinusoidal fashion, out of phase. There was indeed an equilibrium between the two species, but it was a dynamic equilibrium, not a static equilibrium:
As the fox population rises, they eat more hares, which drives the hare population down, causing foxes to starve, driving down the fox population. As the fox population falls, the hare population, with reduced predation, starts to rise. The cycle goes on endlessly. This is a very common dynamic equilibrium, showing up in predator-prey populations, variable stars, pendula – most things that oscillate do so because of coupled differential equations in which one variable responds to the change in another variable.
With that in mind, take a gander at some recent screen shots from BotP:
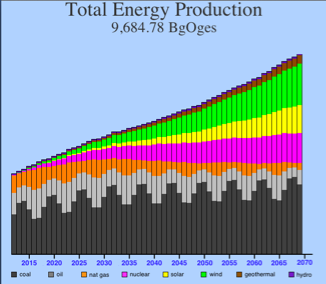
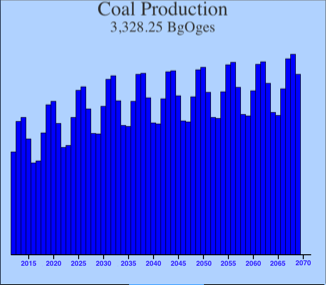
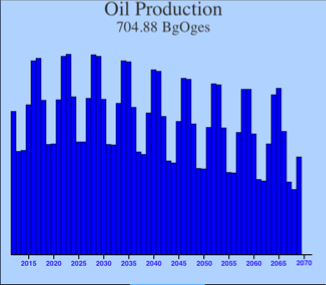
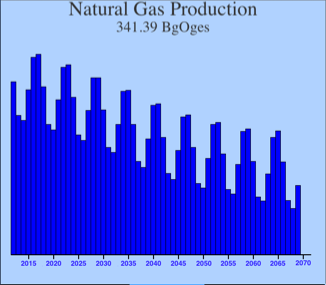
Note that the three fossil fuels are in dynamic equilibrium with each other: the sum of the three in the first graph remains nearly constant. This oscillation arises because my price-seeking algorithm permits some overshoot in utilization of each individual fossil fuel. In other words, the simulation starts with coal production a bit low (according to the pricing coefficients) and oil and natural gas a bit high. Coal responds by jumping up, while oil and natural gas fall. In each case, they overshoot, which sets up the reverse reaction.
The most common solution to problems of this kind is to add “shock absorber” terms to the algorithms that dampen the responses; this produces what’s called a damped oscillation, which eventually settles out. However, in this case, even damped oscillations are unacceptable; I need to flatten out those oscillations fast. To really squash those oscillations, I’d need damping terms so draconian that the system would be unable to respond to real changes in any realistic manner.
There is a better solution: find a more consistent set of initial conditions. The initial conditions consist of the current production of coal and the two coefficients that control its supply. Those two coefficients are difficult to explain; there is an explanation in the December 28th diary. Some of the equations that feed into these equations have been altered, so I can’t just copy over those results, but I think that the trick for now is to adjust the two coefficients so that they match the initial production.
