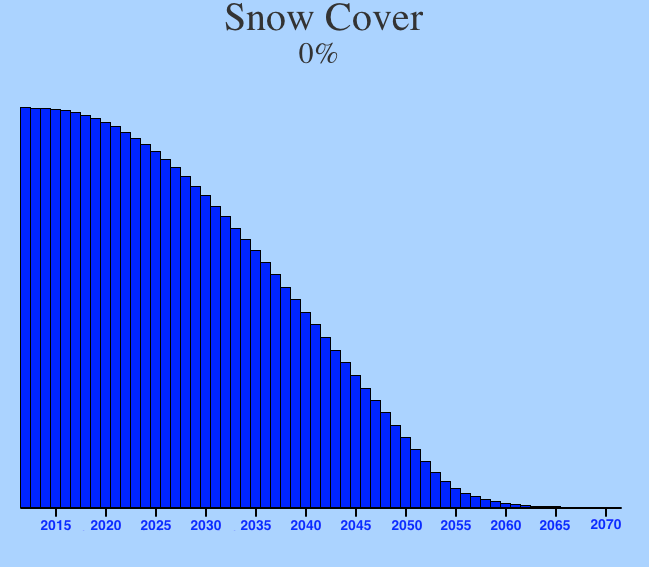
reconciling Snow Cover with Sea Level
Here’s a graph of average global surface temperatures from a recent run of the game:
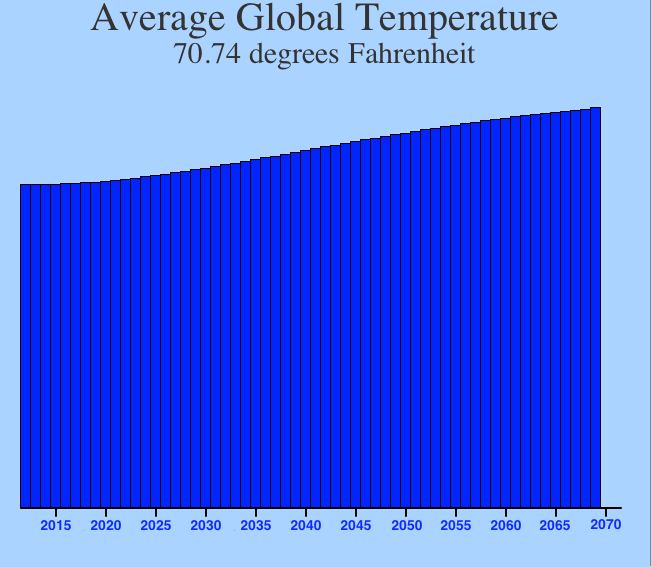
This represents a pretty bad situation: global temperatures have soared. This has cause all the ice in the polar regions to melt:
Here’s the kicker: sea level:
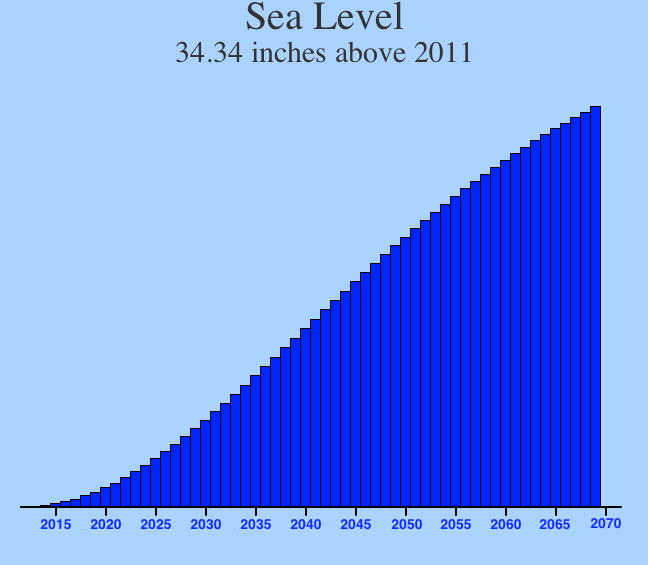
If you know much about climate change, you should be doubling over in laughter at how stupid my algorithms are. Why? Because we know that, if all the ice in the polar regions were to melt, sea level would rise by about 200 meters; this result is about 1/200th of what it should be. Obviously I need to do some work relating average global temperature to sea level. So I dug up some graphs of paleoclimate and came up with this rough set of correlations:
275 mya: -1ºC, -20m
450 mya: +2ºC, 100m
100 mya: +4ºC, 200m
50 mya: +6ºC, 200m
400 mya: +6ºC, 200m
It’s pretty easy to eyeball a linear relationship: sea level = 40m per ºC. But this immediately gets us into a nasty little problem: global temperatures have already risen by more than one ºC, and sea level hasn’t risen by 40m. This is due to thermal inertia; it’s going to take a few thousand years for the ice to warm up enough to start melting in large volumes. There’s also the heat required to melt ice: at 334 J/g, it would take about 1 x 10^25 J just to melt all the ice in the cryosphere. That’s as much energy as the entire solar insolation over two years! To put it another way, if the greenhouse effect were to decrease infrared radiation out from the earth by 1%, it would take 200 years for that effect to melt all the ice in the cryosphere.
So, how do I reflect this in the game? I think that I can use my relaxation algorithm to good effect here. I don’t need to change the control coefficients by much, I just need to relax the melting of the ice. I’ll also rewrite the algorithm for sea level to make it dependent primarily on the melting of ice.
