“Intransitive combat relationships” may sound like a mouthful, but it is nothing more than a formal expression of what most people call “rock-scissors-paper”. Rock beats scissors, scissors beats paper, paper beats rock. The significance of this arrangement is that most combat relationships are transitive: if A beats B, and B beats C, then A beats C. This expresses the idea that the size of the stick you use determines your success. The biggest stick beats the bigger stick which beats the big stick.
Intransitive combat relationships are interesting because success in them requires anticipation of what the other player might use. Of course, the basic rock-scissors-paper game permits no anticipation of the other player’s move, so it is for all intents a random game. However, there are a number of ways to permit some rational anticipation of the other player’s move. A Broderbund game about 30 years ago, The Ancient Art of War, included three types of soldiers with intransitive combat relationships. You maneuvered these soldiers around a battlefield, and knowledge of their positions and movement capabilities made it possible to anticipate your opponent’s likely attacks.
I use intransitive combat relationships in Siboot in dream combat. The player is able to anticipate an opponent’s move by learning what aura-pons the opponent possesses.
In all examples of intransitive combat relationships, three types of unit are used. This seems obvious and natural; however, it is possible to extend the concept to larger numbers of units. This is easily recognized when you use geometric reasoning:
The triangle demonstrates the standard 3-pole intransitive combat relationship; the pentagram demonstrates a 5-pole intransitive combat relationship. The key idea here is to double the number of units affected. In the triangular relationship, each unit beats one unit and is beaten by the other unit. In the pentagram, each unit beats two units and is beaten by the other two units. This concept can be extended to any odd-numbered group larger than 1.
It is also possible to include even-numbered groups, like so:
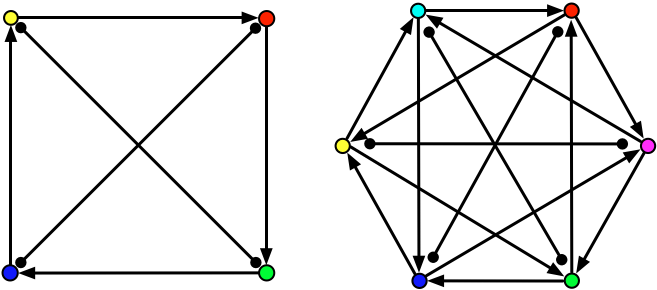
This arrangement requires a new relationship: standoff, denoted by the black circles. The combat system must be able to accomodate this new outcome, which may be difficult in some arrangements.
I shall not be using these ideas for Siboot, as I am already committed to the triangular relationships. However, the concept may of utility in future designs.
