One of the readers of this design diary, Francesco Baro, has been following closely, catching the occasional typo, bad link, or dumb mistake. The other day he sent along two suggestions that set me to thinking. After several days mulling them over, here are my thoughts:
Last Man Standing
Mr. Baro points out that my current victory condition (six auras of the same type) is tricky to achieve because you might not be able to find somebody with the aura you need to win. This could result in some frustration during play. He suggests that instead dream-combat should serve to deprive other people of auras, not accumulate auras for yourself. When an Actor has lost all his auras, he’s out of the game. The process continues until only one person is left, who thereby wins.
This has the big advantage that you don’t have to line everything up perfectly. It also makes combat decisions easier in the early portion of the game: you can pursue one of two strategies: amassing auras for yourself, or depriving somebody else of an aura on which they are short. If you can reduce a player to zero auras of a specific type, then you have critically weakened that player and made it much easier to guess which aura he’ll play.
It does raise a problem, though. Suppose that each player begins the game with nine auras in total, always in the ratio 2:3:4. That gives a total of 63 auras in the game. The winning player must therefore accumulate all 63 auras. That in turn would require that the number system extend up to (at least) 21, so that the player’s auras can be displayed. That also means that the player must win at least 63 dream-battles, which would require a minimum of 32 turns. In practice, it would take far more than that to accumulate the required total. That’s just too long.
One possible solution is to alter the rules of dream combat. Instead of:
A against B: first player takes B
A against C: second player takes A
A against A: no result
we alter it to this:
A against B: first player takes B
A against C: second player takes A
A against A: both auras destroyed
In a purely random game, an average of 2 auras will be destroyed each turn. This should shorten the game – but will it be enough? A purely random game would still take 32 turns to finish.
Perhaps I should reduce the number of auras that the players begin with. Instead of an average of three of each kind, what if I make it two of each kind, with distributions of 1:2:3. That reduces the total aura count to 42.
Loaning auras
This would permit two players to agree to, in effect, join their auras into a single group they could use for dream-combat. The merger would last a single night. This would provide additional capabilities, but there’s a catch to it: the owner of the victorious aura would keep his takings. This wouldn’t do much to help the other player. Moreover, their interests could diverge. Here’s a simplistic example: Player #1 has one B, while Player #2 has one A and one C. They agree to merge. Player #3 attacks Player #1. Player #3, unaware of the merger agreement, plays his A, thinking that Player #1 must play his only aura, a B. Player #1 instead plays Player #2’s A, resulting in the destruction of both A’s. This is a good thing from Player #1’s point of view, because A’s are the only auras that can hurt him. But Player #2 loses his A aura! This could get dangerous.
I think that, for now, I’ll leave off this option.
Later
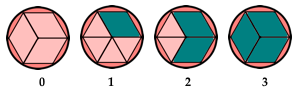
I’ve been wrestling with the problem of displaying the winner’s aura counts. Even if I reduce the total to 2 auras of each type per player, we are still required to display up to 14 auras of each type for the player – and that’s far too big a pile. My current counting system goes up only to six. What to do?
I see two possible solutions. One is to make dream combat entirely destructive, like so:
A against B: B aura is destroyed
A against C: A aura is destroyed
A against A: both auras destroyed
This insures that at least seven auras will be destroyed each turn. If there are 42 auras total, then the game will last at most 6 turns. If there are 63 auras, then the game will last at most 9 turns, which sounds ideal.
The other solution is to permit a player to accumulate auras up to some limit, then begin destroying any excess. That’s prety artificial; I don’t like it.
Numbers
A related problem for me has been the number of quantifiers I permit. The original Siboot permitted positive numbers from 0 to 8. My first plan for Siboot was to include positive numbers from 0 to 6. When I realized that I could apply the negative inflection (the black square) to quantifiers, the range jumped to −6 to +6. But that’s too big: SWAT supports quantifiers from 0 to 10. My thinking now is to confine all quantifiers to the range −3 to +3. This fits inside the constraints of SWAT and has the added benefit of supporting the triangularity concept that I earlier mused about. Here’s what the new numbers would look like: