Light Curves, Part III
I just discovered that the ablation equation that I used in yesterday’s analysis is wrong, wrong, wrong. I applied that same equation to the data from Leonids of length 10 and obtained this result:
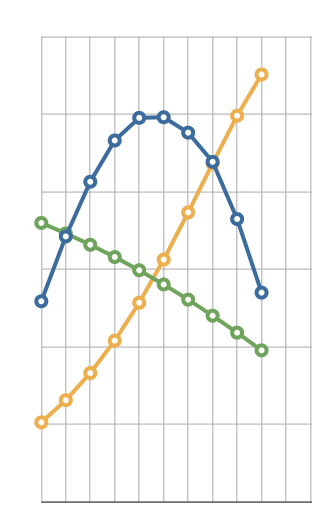
Oops! It turns out that the constant k that I was using in the equation is not constant at all; in order to obtain a fit to the data from the Leonids of length 10, I had to alter it from 6 x 10**13 to 5 x 10**14, which resulted in this graph:
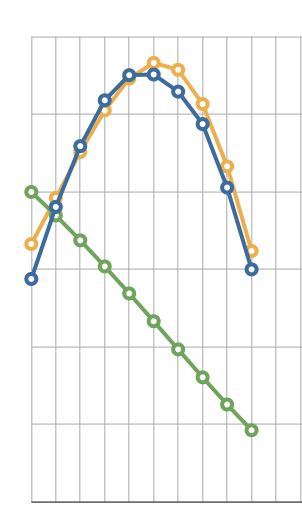
Obviously, if k is not constant, it’s a variable that I haven’t taken into account, and it differs by a factor of 8 between the cases of the Leonids that are 20 flares long and those that are 10 flares long. So much for that idea.
So let’s compare the initial, peak, and final values of the graphs presented in Figure 1 of the March 24th entry:
In each of these graphs, the horizontal axis represents the number of flares in the Leonids being sampled. Thus, each circle represents the average value of all Leonids of a certain length, measured in flares. What to make of these graphs? The first graph suggests that fainter, shorter Leonids start off, paradoxically, with higher initial brightness than the brighter, longer Leonids. The middle graph shows that the brighter Leonids have peak brightness only four times greater than the peak brightness of the fainter Leonids, even though they have, as per Figure 1 in yesterday’s entry, about eight times as much total luminance. This is due to the simple fact that brighter Leonids last longer than dimmer Leonids. Whatever the cause, I think the shape of the curve, not its actual values, is the most important bit of information here. Finally, the rightmost graph certainly shows that, when the big Leonids break up, they show a lot of variation. And the transition from smooth ablation to breakup ablation appears to start around length 15. Is the triggering element here the density of the air or the size of the Leonid? I don’t know.
This concludes my overlong analysis of Leonid light curves. I’m sure that there’s more to look at, but I’m stopping here so that I can move on to the really interesting stuff.
