(Based on my 1990 CGDC Lecture)
Consider the classic diagram for the structure of the play of a computer game:
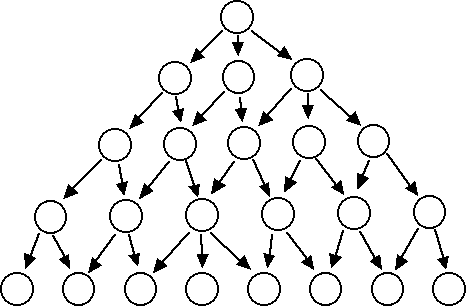
I call this diagram a gametree. It represents the states through which the player can pass in the course of a game. The player begins at the top of the tree and makes a choice which takes him to one of the states in the next level of the tree, which then presents him with a new set of options. He repeats this process until he arrives at an endgame state, which is either a victorious state or a losing state.
Now consider a diagram for the structure of the use of a word processor:
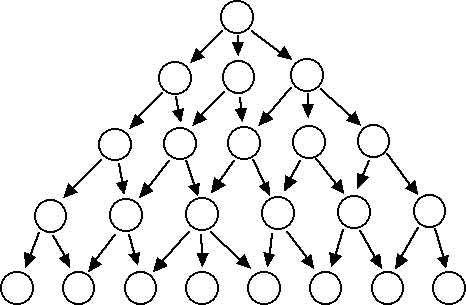
I call this diagram a program tree. The user starts with a blank page and selects a letter to type, which creates a new state, a document with that letter. He then selects another letter to type, which takes him to a new state, and so on until he reaches the bottom of the program tree and his document is complete.
You will note that the structural diagrams for the use of both products are identical.
Differences
But there is a big difference between word processors and games: the former do their job better than games. I use Microsoft Word 4.0 on a Mac, and I am very satisfied with the product. It does everything that I want to do with a word processor, and then some. By contrast, I have yet to play a game that gave me such a sense of satisfaction. Every game I have ever played restricted my freedom of action, refused to permit me to do the things that I wanted to do.
How can it be that games and word processors can yield such different results when they are structurally identical? What is it that word processors do that games don’t do? What do they have that we don’t?
Two new concepts
To answer that question, I shall have to introduce two new concepts. The first is the set of accessible states in a tree. These are all of the states that the user can get to as he traverses the tree. In a word processor, this is the set of all documents that the user could create; in a game, it is the set of all realizable game endings.
The second concept is a little more difficult; it is the set of all expectable states . These are the states that the user might expect to be able to access. In the case of the word processor, these would include all the documents that a user might want to create. In a game, it would include all the game endings that a user might visualize. (I thank Steve Peterson for suggesting that I use the term "expectable" in place of "imaginable".)
A criterion for excellence
I would now like to direct your attention to the ratio of the number of accessible states to the number of expectable states. I suggest that this ratio provides us with a criterion for evaluating the overall merit of a product. Consider that the source of my satisfaction with my word processor lies in the fact that "anything I want to do, I can do." In other words, any state that I expect to access, I can access. The ratio of accessible states to expectable states is very nearly 1. On the other hand, I do not have same experience with games. Many times in games I feel trapped by the design, unable to do the thing that I want to do. In other words, the state that I expect to access is not there. Thus, with games, the ratio of accessible states to expectable states is significantly less than 1.
How can we improve this ratio? There are only two ways to increase a ratio: increase the numerator or decrease the denominator. I shall take up the latter case first.
Decreasing expectable states
This may sound silly at first. How can a designer lower the expectations of his users, short of mass frontal lobotomies? In truth, though, we have a great deal of power, as we set the expectations of our users with the cues we give them. In most cases, sadly, we set them up and then confound their expectations.
Too many designers succumb to overweening pride in creating games that attempt too much. In their eagerness to create an entire world, they toss in features willy-nilly without recognizing the geometrically increasing expectations that such features instill in the users. Whenever you add a new feature to a game, you are suggesting to your users that they might be able to use it in ways that you never imagined. It is incumbent upon you to anticipate all those possibilities and provide for them.
What we need here is completeness of the universes we create. Such completeness is only obtained through closure. A good game design presents a closed and complete universe. Leave out the petty things so that you can do the important features completely. Thus, one desideratum of game design is parsimony. Parsimonious design decreases user expectations.
The user interface manifestation of this problem is the text parser. A parser suggests to the user that any valid English expression will be accepted by the parser. This is a cruel falsehood to perpetrate on a user. We’re programmers; we’re used to the high failure rates associated with command line interfaces. To place this expectation on our users is unwarranted.
Increasing accessible states
I now turn to the happier solution of increasing the number of accessible states. How might we do this? How can we make our gametrees thicker and bushier? A backhanded strategy is to compare games with stories. Here is a structural diagram for a story:
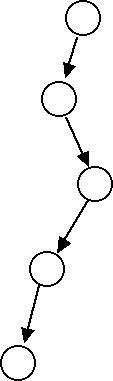
This structure provides graphic representation of the term storyline. A story is a linear sequence of events with just one accessible final state. This suggests that the way to get bushier gametrees is to make them as unstorylike as possible. Unfortunately, negative observations have little utility; we need to know what to do, not what not to do. However, it suggests a convoluted strategy for solving our problem. If a story is the skinny version of a gametree, what occupies the analogous position with respect to the program tree? The answer is a calculation:
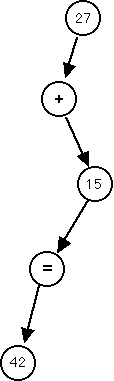
If we examine the progression from linear calculation to bushy word processor, then perhaps we can understand how to build bushier gametrees.
Calculator to word processor
A calculation is most often carried out on a calculator, a device with four arithmetic functions and no memory registers. As we move up the scale, we get calculators with more memory registers, then calculators with indirectly addressable memory registers, then 8-bit microcomputers with 64K of RAM, and lastly my Mac IIx with 8 megs of RAM organized in heaps.
There are several attributes that increase as we move up the progression from calculator to word processor. The first, obviously, is that the program tree grows progressively bushier. There are more accessible states with the more exalted machines. This is expressed both in terms of the number of buttons available to the user (allowing him to specify more states) and the number of displayable states made possible by the increasing display power of the machines in the progression.
There are other attributes that increase as we move up the progression: the computational horsepower of the machines; the number of storage locations available to the user. But the one that strikes me as most important is the indirection of use. The four-function calculator is the most direct, most explicit machine of the set. You punch in a number and crunch it directly, seeing the results directly on the display. As you move up the scale, the number disappears into a memory register, then into one of many memory registers. Later still, with the 8-bit computer, you use a program to talk about the number. With the Mac IIx, you refer to the number by a symbol that holds a handle that refers to a pointer that equals the address of the memory location that holds the number. That’s four levels of indirection!
This suggests to me that indirection might be associated with increasing number of accessible states. I haven’t proven this, of course, but I find the suggestion intriguing. If it be true, how could we increase the amount of indirection used in our game designs?
More and bigger variables
The first tactic we might use is to increase the number of variables we use in our games. After all, a variable is the means by which software utilizes a hardware register. The hardware progression showed increasing numbers of registers, so presumably we should cook up increasing numbers of variables to put into these registers. These variables should also be multi-bit arithmetic variables instead of the single-bit boolean variables so common in computer games. The classic text adventure, for example, has perhaps 50 boolean state variables. These variables can generate 10**15 accessible states. While this may sound like a great many, it compares poorly with word processors. Even a simple one-page word processor with a single font with no stylistic or size variations can generate 10**3600 distinct documents.
Indirect graphics
Games use more graphics these days. Most of the images used, though, are simple bitmaps hand-drawn by artists and blitted onto the screen when needed. This is too direct an approach, and it limits the number of accessible images we can create. A more indirect approach creates images algorithmically. If, for example, we were to devise a room-drawing algorithm, then we could order up rooms to fit any situation, simply passing parameters defining the size, shape, decoration, and function of the room. The same can be said of many of the other graphic elements of our games.
Eschew hard-wired branching
Another overly direct practice is the use of explicitly defined branches in a gametree. All too often, gamers reach points where the designer clearly expects a particular course of action. The code for such situations is a simple IF-statement that rewards the single correct action. This is too explicit. A better solution is to use a more general IF-statement that considers issues more indirectly. For example, instead of "IF the player gives the apple to the horse, then the horse will let the player ride him," we should rather use statements akin to "IF the player satisfies the needs of a nonplayer character, then the nonplayer character will feel gratitude toward the player." This latter form is more difficult to handle; it requires us to define such variables as "needs", "satisfaction", and "gratitude". These variables in turn will imply fairly complex algorithms. Yet consider that the latter form of the IF-statement will handle a great many situations. It can be applied to any nonplayer character. It allows the designer to meet the player’s expectation that all characters have needs and desires. The first form of the IF-statement suggests the possibility of such needs and desires while delivering such behavior in only a single case -- a single accessible state with many expectable states.
