I know a lot of stuff, but I also have a decent appreciation of the stuff I don’t know. Usually, I visualize some areas of knowledge as dark regions that I don’t know about. But I really blew it with Ptolemy. I grossly underestimated the sophistication of his work.
Ptolemy was a late Greek scholar who made many contributions to our knowledge, but his most important contribution was what is now known as the Ptolemaic System, also known as the geocentric model of the solar system. This was the notion that the earth was the center of the universe and that all the heavenly bodies moved around the earth in perfect circles.
Ptolemy did not invent the geocentric model; that had been cooked up centuries earlier. His contribution was to refine it and carry out the detailed calculations specifying its operation. I didn’t know about those calculations. Oops!
The basic geocentric model first had to explain why Venus and Mercury never ventured far from the sun. This was easily explained by specifying that they circled around the sun.
The killer problem for the geocentric model was retrograde motion; I explain the concept here. Ptolemy solved the problem with something called epicycles. It was a hack, but a pretty good hack at that.
The big surprise came when I found a copy of Ptolemy’s main work, the Almagest, on the Internet and downloaded it. Now, although Ptolemy didn’t have trigonometry, he did have a system called chords that permitted him to carry out the same calculations that we would today perform with trigonometry—although not as easily. The chord system was clumsy, but it was adequate. It was rather like a table of sines.
What tripped me up was an image I saw in a book by George Gamow that I read as a boy. It argued that it was all but impossible to divide numbers using Roman numerals, and I still recall the image of a Roman in a toga trying to carry out a long division using Roman numerals. I have therefore believed throughout my life that you simply couldn’t do much in the way of calculation (beyond addition and subtraction) using Roman numerals. It turns out that I was wrong; the Egyptians developed an interesting algorithm using doubling and halving. Here’s how it’s done with multiplication:
Make a table with two columns, and enter the two numbers to be multiplied into the first row. Make the next row by halving the first number (discarding remainders) and doubling the second. Continue until there is nothing left to halve. Cross out all the rows where the left number is even. Add the remaining numbers in the second column. The result is the product of the first two numbers. (Here’s the source.) Here’s an example using both Hindu numerals and Roman numerals:
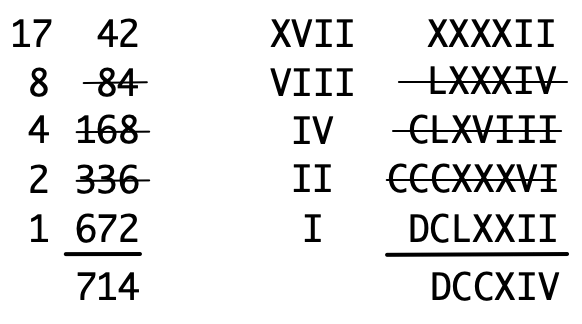
As you can see, this really isn’t much harder than multiplication the way we do it. However, division is another story; it’s more difficult.
Thus, I was wrong to think that the Romans and Greeks couldn’t multiply and divide. This in turn means that Ptolemy was in fact able to carry out calculations of the motions of the planets to support his geocentric model of the solar system. And support it he did! Here’s a single calculation from the Almagest:
With these data, let the moon’s eccentric circle be ABG on center D and diameter ADG, on which E represents the center of the ecliptic. On center B draw the moon’s epicycle, ZH0. Let the sense of motion of the epicycle be towards the rear from B towards A and the sense of motion of the moon on the epicycle be from Z towards H and thenceforth to Θ. Join DB and EΘBZ.
Now in a mean [synodic] month occur two revolutions of the epicycle on the eccenter, and in the situation in question the elongation of mean moon from mean sun was 315º 32'. So if we double the latter and subtract the 360° of a circle, we will get the elongation at that moment of the epicycle from the apogee of the eccenter, counting towards the rear; this is 271º 4'.
Therefore angle AEB = 88º 56'. So drop the perpendicular DK from D on to EB.
Therefore angle DEB = 88º 56'
Therefore in the circle about right-angled triangle DEK, arc DK = 177º 52’ and arc EK = 2º 8’
Therefore the corresponding chords DK = 119º 59’ and EK = 2º 14'
Therefore where DE, the distance between the centres, is 10º 19' and DB, the radius of the eccenter, is 49º 41',
DK = 10º 19' and EK = 0º 12'
But BK squared = DB squared - DK squared.
therefore BK = 48º 36'
and, by addition, BE = 48º 48’.
Thus, the Greeks were certainly capable of carrying out sophisticated calculations. However, there remains a distinction that is crucial to understanding why the Greeks never truly developed science. Ptolemy’s work was entirely geometic in nature. That is, he began with geometry, which the Greeks had figured out in great detail, and then carried out strictly geometic calculations. This is very important in understanding the contribution of the Oxford Calculators 1300 years later.
January 26th, 2020
