Global Dilemma (my title was Guns & Butter) was not one of my better games. It had some severe problems integrating economics with the military portion of the game. But it did contain a number of elements of which I am proud. One of these was the continent-generating algorithm. World-building routines have been part of a number of games: Seven Cities of Gold, Starflight, Empire, and others sported world builders. The basic task is simple to state: generate a unique terrain map from a random seed, insuring that the map contains interesting yet functional terrain. Achieving it, however, can be quite a challenge.
For Guns & Butter, I wanted to make a world-builder that would go beyond current technology, a world builder that would support complex terrain types yet look good and not concoct impossible terrain. In this article, I will describe the world builder that I designed.
Specifying a world
I began by determining that my world would consist of a single continent. My game did not need naval forces and I thought it best to avoid the complication of maritime rules. Next, I defined the size of the rectangle into which the continent would fit. The continent itself would be composed of fundamental units called provinces. Each province would be an irregular region with a single city as provincial capital. Countries would be collections of provinces. Straight roads would connect adjacent provinces, but not all contiguous pairs of provinces would be connected by roads.
To lay down the continent, I simply laid down provincial capitals randomly. My random number generator randomly selected points in the available space, the only restriction being that no new point could be placed within 64 pixels of an already existing provincial capital. This prevented overcrowding of provincial capitals. I laid down 64 provincial capitals. These were the skeleton of the nascent continent.
With the capitals in place, my next task was to form the provincial boundaries. The boundaries had to divide up the existing territory among the various provinces, and then assign nicely meandering boundaries. After all, provinces that look like polygons would never do. I decided to tackle the problem in two steps: first, to assign polygons that divided the territory, then "meanderize" the polygon sides.
Drawing the polygons
The task of making a clean set of polygons out of a set of points is quite tricky. After I had solved the problem, I discovered that it is addressed in Sedgewick Algorithms, 2nd Edition, pp 408-410, although his discussion is even more hand-waving than this essay.
The problem can be simplified by casting it into a different form. For the set of cities, create a set of spokes connecting the cities such that 1) all cities are connected by spokes; 2) no two spokes cross each other; 3) every pair of cities that could be connected with a spoke is connected with a spoke and 4) the total length of all spokes is minimized. I’ll show you how these spokes can be used to make provinces later. For now, I shall concentrate on building the spoke set. Consider the following diagram:
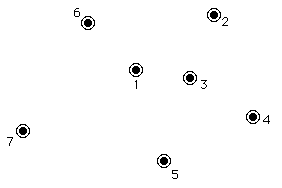
I shall create the spokeset for City 1. I first create a list of the nearest cities, ranked in order of their distance from City 1. In this case, the list has cities 3, 6, 2, 5, 4 and 7. Starting at the top of the list, I begin adding cities to the spoke set of the City 1, but two factors could exclude a city from the spoke set. In this case, Cities 4 is masked from inclusion by City 3. The spokes are too close together and the subsequent border will be too seriously deformed. Therefore I must reject City 4. The obvious way to do this is to calculate spoke angles and look for spoke angles that are too close together. As it happens, the use of trigonometry in this calculation is prohibitively slow, so I used another, more complex system that runs faster. This other system is too messy for me to explain here. It used analytic geometry to calculate whether any of a set of lines intersected.
Building a province from spokes
The result of all this calculating is a set of spokes for each city on the map. Those spokes break the space of the continent up into triangles. This is important, as quadrilaterals will cause this algorithm to fail. Note that condition 3) of the above set of requirements for spokes insures that all the shapes formed by the spokes are triangles. To form a province around a city, we create two sets of midpoints: the midpoints of the spokes themselves, and the midpoints of the triangles. We connect all these midpoints to make a province:
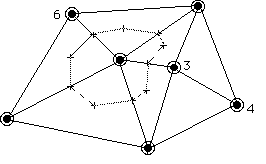
Randomizing the province boundaries
We now have a set of polygonal provinces. The borders are straight lines, which looks much too artificial. We need a reliable way to make those borders wiggle realistically. Moreover, there’s a nasty restriction: we have to have the same wiggling on both sides of the border. That is, when we create each province’s final shape, the zigs and zags of its border must match the corresponding zigs and zags of its neighbor’s border. This, it turns out, is a major problem.
My solution to these requirements was to create a deviation table 1,024 elements long and stock it with random numbers between -7 and +7. The algorithm begins at one vertex of the polygon and prepares to walk down the edge of the polygon. First it selects the starting table index from the deviation table that it will use. This selection is based on the coordinates of the vertex and the direction (clockwise or counterclockwise) in which the polygon is being drawn. This guarantees that the same deviation table entries will be accessed regardless of which side of the border is being drawn. This is what insures that we get matching borders for the two adjacent provinces. This trick also insures that different sections of the deviation table are used to draw different borders, so there will be no telltale pattern to the deviations.
The algorithm takes many small steps down the polygon edge towards the next vertex, at each step wiggling the border in the x and y dimensions by the amount given in the deviation table. The result of all this is a beautifully irregular province.
Adding mountains, forests, and deserts
My final task was to add terrain features: mountain ranges, forests, and deserts. I decided that I wanted these terrain features to act as apparent blocks to roads connecting provinces. You will recall that all adjacent provinces are connected by spokes. Well, not all spokes became roads. Some spokes are left empty. The spaces created by these non-road spokes are the spaces that I wanted to fill with terrain features.
To define these terrain regions, my algorithm traces a complex polygon by laying down a right-handed path. It first grabs some non-road spoke. It then lays down an initial point one-quarter of the way down the non-road spoke.
If the spoke on its right is not a road spoke, it draws a line to the one-quarter point on that spoke. It continues this process until it encounters a road spoke. When that happens, it draws a line to the midpoint of the province polygon edge emanating from the road spoke. It continues drawing to the midpoint of the line connecting the city in the opposite province to the end of province polygon edge which it had just bisected. The process described in this paragraph is iterated until the algorithm returns to its starting point.
The result is a polygonal region occupying the non-road areas between provinces. Depending on whether it is a forest, a mountain range, or a desert, I randomly scatter the appropriate icons inside the region. Although they are created in random order, they are drawn from top to bottom so that the base of one mountain or tree does not obscure the top of a lower one.
Results
A typical end result is shown below. As you can see, the continent is quite pretty. It takes about five minutes to build this continent on a Mac Plus.

