August 15th, 2010
This algorithm is not of my design; indeed, it is quite old, and I’m sure the computer scientists have a better name for it. Let me explain the basic algorithm as I first encountered it. You may recall the Edgar Allen Poe story “The Gold Bug”, in which a fellow cracks a coded note by using frequency tables for letters in the alphabet. For example, “e” is the most frequently appearing letter in the alphabet; thus, the character that appeared most frequently was likely an “e”. By extending this downward to the other characters, he was able to crack the code (a simple one, to be sure) and decode the message. In order to apply this technique, you must know the letter frequencies of the 27 letters of the alphabet (space counts as the 27th letter). Here’s a bar graph showing those frequencies for the English language, courtesy of Wikipedia:
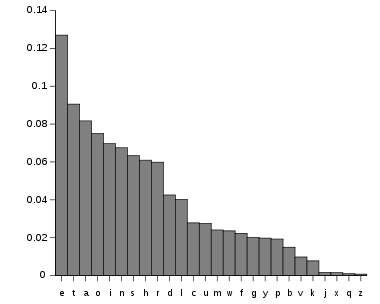
You could turn this table around and use it to generate “English-like” text: that is, text that has the same letter frequencies that you get in the English language. Here’s how:
Use your random number generator to pick a number between 0.00 and 1.00. Look up that number along the scale along the bottom, then write down the letter above it. Now repeat the procedure many times (in this case, it won’t work, because this scale doesn’t show the space character. Play along with me here, please!) When you’re done, you’ll have a long string of letters that don’t make any sense at all. This doesn’t look life a useful algorithm, does it?
But now we bring in a new trick: let’s build a new frequency table, using not individual letters, but pairs of letters. This will be a big table, to be sure: there will be 729 entries in it. But that’s what computers are for! So we write a computer program that scans tons of English text and prepares a table of frequencies of each letter pair. Then we use the same random number scheme to pick out couples, except that this time we do it a little differently. With the very first letter in our string, we use the simple one-letter frequency table to randomly pick a letter. Then we use the selected letter as input into our two-letter frequency table, asking, in effect, “Given that the first letter of the pair is this one, what are the probabilities of each letter being the second letter of the pair?” For example, if the first letter of the pair is “Q”, you can be almost certain that the second letter will be “U”. If, on the other hand, the first letter of the pair is “P”, then the odds of the second letter being “M” are very low, while the odds of the second letter being “E” are much higher.
So now we’ve chosen a second letter. Now we use the same procedure to pick a third letter, using the second letter as an input. Then we do it for the fourth letter, using the third letter as the input, and so on and on. The result we’ll get might look a little more English-like, but it’s still not very good.
But why stop at two-letter frequency scheme? Why not use 3 letters, with 19,683 entries? Or 4 letters, with 531,441 entries? These can easily be handled by a computer. And in fact, that’s exactly what I did back in 1988 when I was writing the computer game “Guns & Butter”. I had a spiffy map generating algorithm, and I wanted an equally spiffy algorithm for naming the cities on the map. I decided to use the Turco-Mongol languages for my base, because they’re exotic, they have a strong “feel” to them, and minor mistakes that would ruin straight English-sounding names would not be noticeable in this foreign setting. So I entered as many Turco-Mongol names as I could and ran a program that built the frequency tables. Unfortunately, because of memory limitations at the time (many computers had 4 or 8 MB of RAM, I couldn’t use the 4-letter sequences for want of RAM, but I did use 3-letter sequences, and here is a sample of the output of that algorithm:
Kabinongot, Yushin, Kamangri, Bakirksh, Ogalymamus, Malda, Tuna, Turte, Bogdigizer, Jakset, Murbihuzde, Imuji, Aniboorkha, Vigizirgin, Drot, Shaisakhat, Kerigin, Toqusecbad, Yumyshuksa, Yatoquc, Botoqtambu, Mohi, Tushai, Vogarnis.
Every one of these names is pronounceable -- that’s quite an achievement! Obviously, if I had gone up to four-letter sequences, it would have been much better. But nowadays our computers are much bigger and faster: a 6-letter frequency table would require less than 400 MB of memory. With frequency tables that big, you could really do some impressive work. Of course, you might get well-formed words, but you still wouldn’t get readable sentences.
But this line of thinking doesn’t stop here, because the basic extrapolation algorithm can be applied to ANY sequence of information that follows some reasonably rule-based system. The obvious application would be to music. After all, music is just a sequence of notes, right? Well, no, it isn’t. There’s a lot more to music than just notes. In the first place, each note has a different duration, so you’re not only using, say, 88 notes (as from a piano), but you must also specify their duration in, say, 10 steps. And you mustn’t forget amplitude levels, either. There’s a big difference between a soft note and a loud note. Thus, each and every note could assume any of, say, 10,000 different configurations. Which means that, to get a two-note frequency table, you’d need 100,000,000 slots in your table. You see the problem?
It’s possible to cut corners by specifying that amplitudes and durations fall on binary divisions, so we can have a sixteenth-beat note or a quarter-beat note, but not a three-sixteenths-beat note. And we could also cut things down a bit by acknowledging that nobody ever goes from the very top of the scale all the way down to the very bottom of the scale. With this, would could dramatically reduce the size of our frequency tables. Even so, we’d have a difficult time getting above four-note sequences -- and most music has fundamental components that are longer than four notes. So music generation by this extrapolation algorithm isn’t yet possible. However, I wouldn’t rule out the possibility of some sharp musician coming up with a scheme that involves simplifying assumptions and makes it possible. Staying within, say, three octaves, should be possible. Even then, however, you’re still not taking into account attack, sustain, and decay parameters for notes or overtones or the voices of the different instruments -- we’re still talking really primitive stuff here.
But there are still plenty of other applications of this algorithm. Consider this list of the 500 most frequently used words in the English language. We could build a four-step frequency table for these words with just 125 Gigabytes of storage. This is definitely within the reach of personal computers, and could provide the basis for an English sentence generator. These sentences still wouldn’t make sense, but they might be interesting.
