I have referred to this algorithm many times in my lectures, but I have never explained the details. I present the algorithm here as an example of obsolete technology.
Back in 1979 I was working at Atari on my first game for the Atari 2600, the videogames machine. It had a 6502 CPU, which was an excellent design. However, it was an eight-bit CPU, which by modern standards is hopelessly limited. It ran at 1 MHz, thousands of times slower than modern CPUs. Also, it could not multiply or divide; addition and subtraction were the only two arithmetic operations it could execute. It could also double and halve numbers, but with 8-bit words, that won’t take you very far.
Here’s a screenshot of the game I was working on:

The player is the bright yellow guy at the bottom; his antagonist is blue cross near the center of the window. That cross spins during play.
The key conceit of the game is “hidden movement”: the player does not see through walls, so the antagonist is visible only when the a clear “line of sight” can be drawn between the two characters. But tracing a line of sight requires the program to figure out the line between the two characters. This is algebraically trivial; the formula for a straight line is:
y = mx +b
where y is the y-coordinate of a point on the line, x is the x-coordinate, m is the slope of the line, and b is the offset. There’s a problem with this: the equation requires the computer to multiply m by x, and the 6502 can’t multiply. The lack of multiplication and division limited games on the 2600 to lines that were horizontal or vertical or at 45º angles. A few games could also do 30º angles [because sine(30º) = 0.5]. But there was no way to process lines at arbitrary angles. That was the problem I sought to solve. Here’s an example for an easy case:
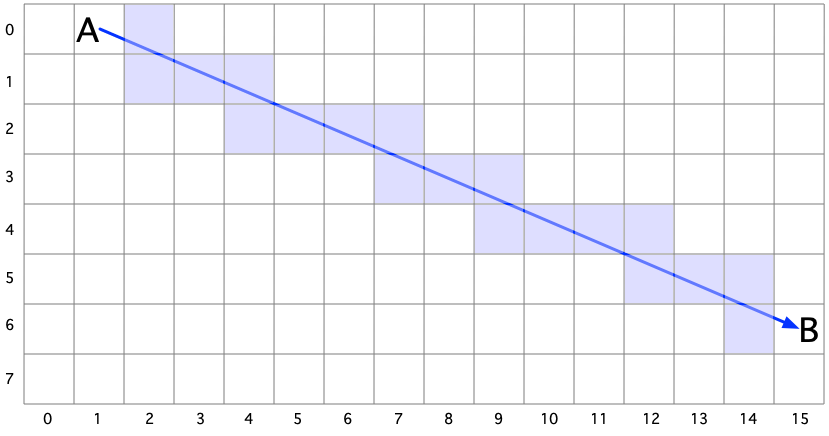
I want the computer to be able to draw a line from point A to point B. It needs to calculate the coordinates of each of the blue squares. Here’s an old-fashioned flow chart showing the algorithm:
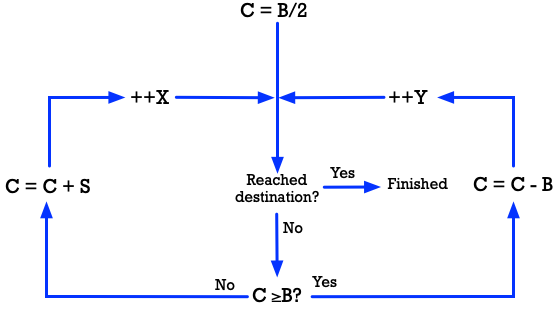
The terms used are as follows:
DeltaX: the difference between the X-position of one point and the X-position of the other point
DeltaY: the difference between the Y-position of one point and the Y-position of the other point
B: the larger of (DeltaX, DeltaY)
S: the smaller of (DeltaX, DeltaY)
C: an accumulator
X: the X-position of the current square in the line
Y: the Y-position of the current square in the line
Here is the output of the algorithm applied to the image above:
Now, the real-world implementation of the algorithm is a bit more complicated. There are four quadrants to consider, each one with its own logic as to whether X or Y should be incremented or decremented. In the game, I had to consider in addition the presence or absence of walls that might block the line of sight. The final result took about 150 lines of assembler code.
Now you will ask, what does any of this have to do with Mayan arithmetic? The Mayans started off with a simple question: how long is the year? All early civilizations faced this question, because it was crucial to figuring the agricultural schedule. You can’t rely on the weather alone to decide when it’s time to plant; you must have something else to guide your decisions. That something else is a great technology called “the calendar”. It didn’t take long to figure out that the year is about 365 days long. However, because the real year is longer than 365 days, their calendar drifted out of synch with the real year. Eventually they figured out that the error was about one day every four years. But how could they express this idea? They couldn’t say that the year is 365 and one-quarter days long — they didn’t have multiplication or division, so they could not conceive of a fraction. Similarly, they couldn’t specify it as 365.25 days long — again, without the concept of division, this makes no sense.
Their solution was to say that there are 1461 days in 4 years. This expression requires no fractions and no division. They applied the concept to other mathematical problems. This way of thinking about it leads directly to our formula for leap years: every fourth year, add one day to the year.
This basic idea can be extended to any ratio. Suppose, for example, that they determined that there are 3288 days in 9 years (each year being considered to be 365 days long).
The Egyptian Algorithm for Division
I recently learned (only a few thousand years later) that the Egyptians developed an algorithm for division that uses nothing more than addition and doubling. Here’s an example of the algorithm in use. First, prepare a table showing nothing but powers of two. We shall divide 1766 by 51.
Next, enter the divisor into first row underneath “X”:
Fill in the “X” column by doubling the cell values as you go down:
I stopped the doubling process in Row 5 because the next value, 3264, would have been greater than the dividend (1766). The next step is to transfer (in the bottom row) the second and third column values:
Now we work our way back up the table, row by row. In each row, we add the X-value to the current value of Sum, and if the result exceeds the dividend, then we skip that row. But if the X-value in that row added to the Sum produces a result less than the dividend, then we replace the sum with the new sum and add the corresponding value in the 2**N column to the quotient. It’s easier to understand just by looking at the sequence:
This leads us to conclude that 1766 divided by 51 is 34, with a remainder of 32. I really wish that we had known of this algorithm back in 1978 — we could have carried out division on the 6502!
