Interactive Storytelling Tools for Writers

Most people think of simulation as very serious business, requiring hundreds of thousands of lines of code expressing very complex mathematical and scientific concepts. Yes, many such simulations are masterworks of erudition. But lack of knowledge never stopped me; I built an airplane out of cardboard when I was 13 years old and would have launched it from the roof—with me inside—had the rain not ruined my cardboard airplane. At roughly the same age I experimented with wires stuck into the electrical outlets, giggling maniacally as the wires turned red and vaporized. I’ve carried out all sorts of idiotic projects, most of which failed miserably—but when they worked, everybody thought I was a genius. I have learned how to slap together simulations of lots of things. None of my simulations would earn anything more than derisive laughter from the experts. But most of them were good enough for use by non-experts. In this lesson, I’ll describe some of the simulation games I’ve concocted.

Although I call myself a dilettante, I actually did a great deal of research for each of my simulations; I’d read at least a dozen books on the subject, some of which were quite technical in nature. 

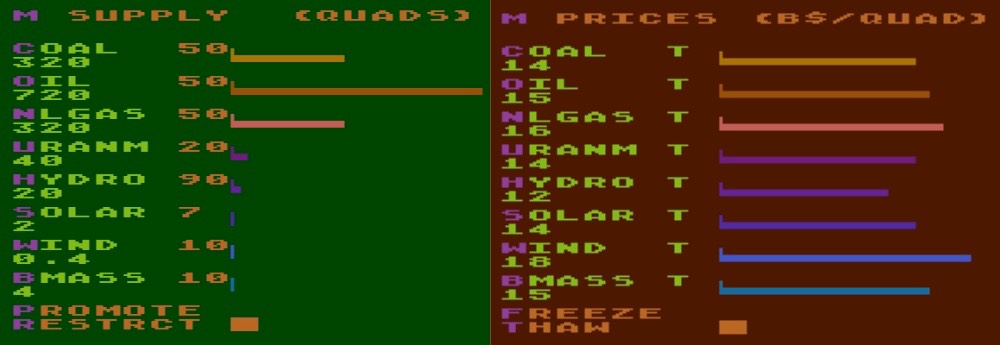
Energy Czar
This was an educational game for the Atari Home Computer. You can find a good description here. It used a simple set of equations. It included as variables the following energy sources: coal, oil, natural gas, nuclear power, hydro-electric, solar, wind, and biomass. For each of these, the model calculated the supply, demand, and price from simple economic formulae as well as my numbers for supply as a function of price. The player could set a tax on each source of energy to depress demand for that energy source. Each energy source also generated some degree of pollution that killed a certain number of people. The overall results affected economic growth and inflation, leading to changes in public opinion of the player’s performance. All in all, the simulation entailed a few score equations. 

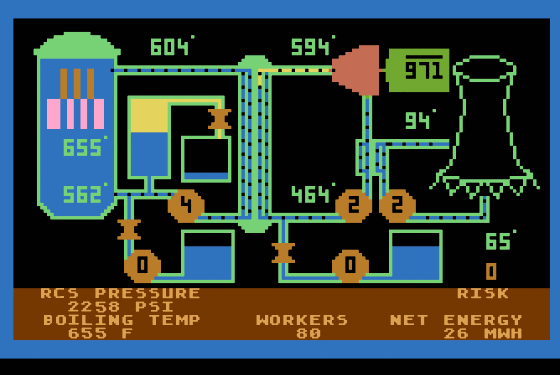
Scram
This was a nuclear power plant simulation. I happened to know from previous jobs a great deal about nuclear power plant operations, and I had read the technical reports on the accident at the Three Mile Island reactor. The simulation was really a simple application of Newton’s law of thermal transfer: the amount of heat transferred from a higher temperature source to a lower temperature sink is proportional to the difference in temperatures multiplied by the thermal conductivity of the surface between them. In mathematical terms:

Heat flow = Thermal Conductivity * (higher temperature - lower temperature)

Pretty simple, huh? There were just three places where this equation was used: in the reactor core (pink), the steam generator (the blue-green vertical object in the center of the display), and the condenser (the little thingamabob just above the pair of 2’s in orange). There were also some valves (orange X-shapes) and pumps (orange octagons) to operate. The player had to dead the temperatures at various points (in green) to figure out what was happening in the reaction. All very simple stuff. The hardest part of programming was getting the bubbles in the steam generator (little black dots) to move properly. 

Tanktics, Legionnaire, and Eastern Front (1941)
These were all wargames, and as such they did include some minor simulation elements in the calculation of combat results. Generally, combat results systems for strategy wargames rely on calculating the ratio of strength of the attacker to the defender. That ratio then determines the proportionate losses of the two forces. 

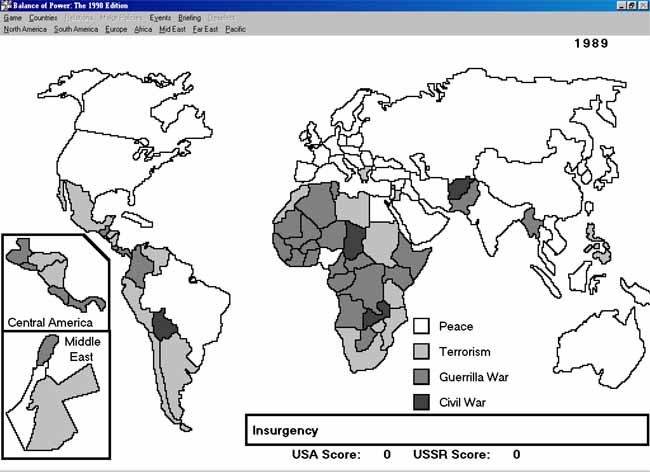
Balance of Power
A lot of research went into the design of the game; I have about two dozen books that I read during research for the game. I wrote an entire book explaining in detail the simulation system used in Balance of Power; you can find that book here on my website. Unfortunately, at that time, floating point calculations were difficult to execute on personal computers, so I had to use integer arithmetic, an ancient form of calculation that is about as useful today as knowing how to drive a chariot. How times have changed. This is an excellent source if you wish to learn about simple simulation.

Balance of the Planet
This is my largest simulation. I made the first version in 1990 and self-published it. You can download it here. It is written in Java; if there’s enough demand, I’ll make the source code available. 

I developed a number of nice innovations for Balance of the Planet. One which is irrelevant to this discussion is the multi-slider system; here’s a screenshot:

By sliding the four gray thumbs back and forth, you can allocate different amounts to each of the five recipients in the game. This screenshot shows the biggest allocation to Public Transport, and the smallest to Education. 

The simulation uses over 80 variables that are related to each other in a complex mesh; their equations are all handled as separate methods in the source code file Model.java. That creates a new problem that can be especially difficult for beginners: how to balance the system. When you create a system with a lot of interconnected equations, and then run it for the first time, you’ll find that several of the variables in the system will go wild with crazy results: numbers that are absurdly high or low. Making such a system work can feel like herding cats. So how do you go about balancing all those equations? 

It’s really not that hard, but it does require a lot of dogged effort. You start by identifying any variable that has gone crazy on you. Then you look at the variables that act as inputs; if any of those went crazy, then shift your attention to that variable. Keep following the trail backwards until you reach the source of all the trouble, the variable that had reasonable inputs but produced a crazy output. 

Now that you’ve identified the problem, you have to figure out how to fix it. The equation has reasonable inputs but is producing a number that is way out of bounds. Let’s say that it is too big. In that case, your simplest solution is to scale it down with a coefficient. In other words, replace this:

Result = first input + second input;

with something like this:

Result = 0.1 * (first input + second input);

In other words, multiply it by a number less than 1. That’s the simplest solution, and it might be good enough. But if it isn’t good enough, then you’ll need to take stronger measures, such as taking the square root:

Result = Sqrt(first input + second input);

or even a log:

Result = log(first input + second input);

If you need to scale up a number that’s too tiny, then either a) multiply by a number greater than 1; b) take the square of it; or take 10 to its power. 

The odds are, though, that you’ll find lots of equations that need tuning. Some results might not be crazy, but they’ll still be too big or too small. Just keep working back to find the original source of the problem, then adjust it as necessary, and continue until the entire system is working nicely. 

Rocket Science
I slapped this thing together in JavaScript maybe six years ago. You can find the game here and directly examine the JavaScript code to see how I handled this simple simulation. The tale of how the game came to be is here. It has some useful lessons.