Let’s run through a few examples showing how to use BNumber math. Let’s suppose that Joe tells Fred that he (Joe) likes Mary this much: How_Much. In other words, Fred declares that
pBad_Good[Joe][Mary] = How_Much
Now, Fred is no fool and he’s not about to believe Joe completely. His trust in Joe is less than absolute. Suppose that we want to calculate how Fred interprets Joe’s statement. In other words, we want to calculate the change in cBad_Good[Fred][Joe][Mary].
Obviously, we’re going to start with the original value of cBad_Good[Fred][Joe][Mary] and then move it part of the way to How_Much. Our question is, how far do we move it? The answer should be obvious: the distance we move it should be determined by how much Fred trusts Joe: pFalse_Honest[Fred][Joe].
One of the first lessons I learned in physics was “when figuring out a problem, start by drawing a picture of the situation”. I’ve developed a simple graphical way of representing problems the BNumbers. We start with a standard BNumber line representing all the possible values of cBad_Good[Fred][Joe][Mary]. We place the initial value of cBad_Good[Fred][Joe][Mary] as well as the value that Joe declared as How_Much. I’ll just make up some numbers for this example:

It should be obvious that the distance we move from the original value of cBad_Good[Fred][Joe][Mary] to How_Much should be based on how much trust Fred has in Joe (pFalse_Honest[Fred][Joe]). If Fred doesn’t trust Joe one bit (pFalse_Honest[Fred][Joe] = -0.99), then Fred shouldn’t change his value of cBad_Good[Fred][Joe][Mary] one bit. If, on the other hand, Fred trusts Joe completely (pFalse_Honest[Fred][Joe] = +0.99), then Fred should correct his old, obviously obsolete value and move all the way to How_Much.
Here’s how I diagram that reasoning:
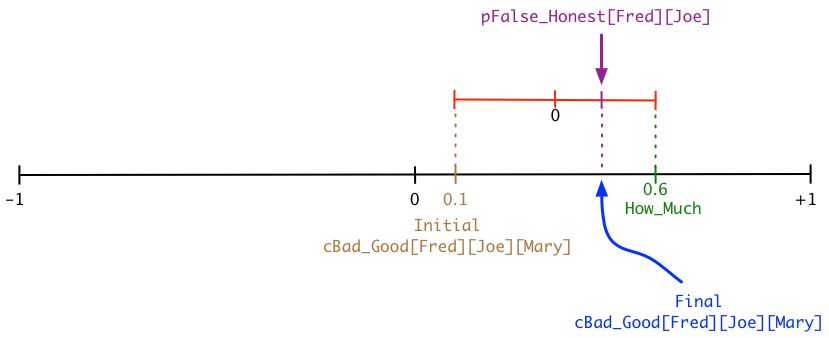
There are three input values here: initial cBad_Good[Fred][Joe][Mary], pFalse_Honest[Fred][Joe], and How_Much. Here’s the Blend formula expressing what’s in the diagram:
cBad_Good[Fred][Joe][Mary] = Blend(cBad_Good[Fred][Joe][Mary], How_Much, pFalse_Honest[Fred][Joe])
A Slightly Harder Example
Suppose that Mary likes Joe (pBad_Good[Mary][Joe] = 0.2). Joe does something nice for Mary (takes out the garbage, does the dishes, something like that). How will his nice action change pBad_Good[Mary][Joe]?
First we must express the niceness of the act in mathematical terms. We should follow our standard protocol and use a double label here: Nasty_Nice. This covers both nice acts and nasty acts. A nasty act will have a negative value of Nasty_Nice, while a nice act will have a positive value.
The obvious solution is to simply add the Nasty_Nice value of the act to pBad_Good[Mary][Joe]:
pBad_Good[Mary][Joe] = BSum(pBad_Good[Mary][Joe], Nasty_Nice)
This makes all sorts of sense. If Nasty_Nice = 0, then there’s no change in pBad_Good[Mary][Joe]. If Nasty_Nice < 0, the Mary will like Joe less and pBad_Good[Mary][Joe] will be reduced. And if Nasty_Nice > 0, then Mary will like Joe more and pBad_Good[Mary][Joe] will be increased. Here’s the diagram for the BSum process:
But there’s a catch: doing nice acts doesn’t absolutely control people’s feelings. Sure, Joe could give Mary a million dollars (Nasty_Nice = 0.999), but that doesn’t mean that Mary will adore Joe ever after. We need to scale down the magnitude of the effect. We can do that with Blend and Mary’s aBad_Good value. Here’s how to diagram the scaling-down process:
This translates to the following formula:
pBad_Good[Mary][Joe] = Blend(pBad_Good[Mary][Joe], BSum(pBad_Good[Mary][Joe], Nasty_Nice), aBad_Good[Mary])
