This is probably my worst vice as a designer: I always aim too high, trying to build systems that are just at the upper edge of what I can fully grasp. I then spend weeks trying to make them work, and often end up throwing up my hands in despair. Today’s essay presents an example of this vice at work.
Here’s the issue: Joe tells Mary that Bob has 2 Tanagagons, but his uncertainty about this number is -0.5. Mary currently thinks that Bob has only 1.2 Tanagagond, with uncertainty of -0.2. How should Mary alter her estimate of Bob’s Tanagagons in response to this item of news? Here’s the current algorithm:
(The editor for my website manager, Sandvox, is too stupid to be able to correctly handle a simple copy and paste from the program listing — hence I paste a screenshot of the code.)
So here we have 80 lines of code that recalculate DirObject’s P2 value of the trait. Yes, it’s a tricky algorithm. Indeed, it’s so tricky that, when tracing its behavior, I find oddities that are not quite up to my expectations. There’s one small bug in the code, but I don’t think that it affects the results significantly, and it would be a bit messy to correct.
Part of the problem is the incrementally adjusted netMean. That’s just wrong, but I didn’t think that the difference between my incremental method and the correct parallel method would be significant. But do I really know that?
Once again I have bitten off more than I can chew. I must now throw this algorithm away and settle for something simpler, something neater, something easier to understand. This ‘something’ will also be considerably more stupid, and that won’t sit well in my stomach. But I’ve got to learn to stop overreaching.
Where to begin? Here’s a very simple algorithm: adjust the existing P2 value by the reported P3 value scaled by our trust in the reporter. In other words:
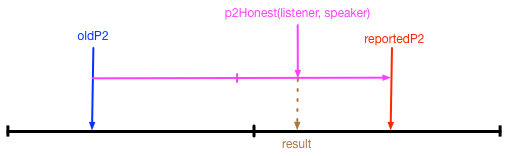
newP2 = Blend(oldP2, reportedP2, p2Honest(listener, speaker))
That gives too much weight to the reporter; I need to scale down the effect, like so:
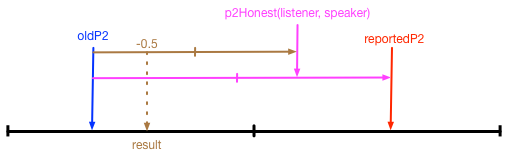
newP2 = Blend(oldP2, reportedP2, Blend(-0.999, p2Honest(listener, speaker), -0.5))
That’s pretty simple, but it fails to take into account the current uncertainty value of the oldP2. How about this change:
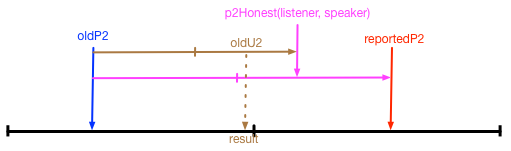
newP2 = Blend(oldP2, reportedP2, Blend(-0.999, p2Honest(listener, speaker), oldU2))
That’s pretty good. Simple, easy to understand. But what about the reported U2 value from from the speaker? That should also be included. I think that it should be combined with the oldU2, like so:
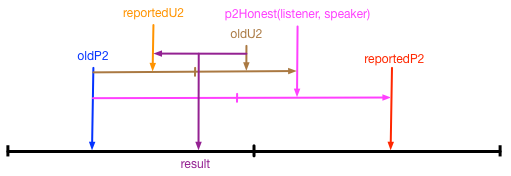
newP2 = Blend(oldP2, reportedP2, Blend(-0.999, p2Honest(listener, speaker), Blend(oldU2, -reportedU2, 0)))
There remains another issue: how should I alter p2Honest(listener, speaker)? I would think that the discrepancy between oldP2 and reportedP2 should be used to scale down p2Honest(listener, speaker). Hence:
p2Honest(listener, speaker) = Blend(oldP2Honest, BAbsVal(BDifference(oldP2, reportedP2)), 0)
But I am unhappy using the BAbsVal-BDifference combination. Technical purity requires me to use some kind of Blend arrangement. This may not be possible; I sense that Blend can’t handle differences between values without using a subtraction. For now, then, I suppose that I shall stick with the above formula.
