Last night’s run came out looking pretty good, except that there were still about 20 false positives out of 245 reported Leonids. That’s completely unacceptable, so I searched for the most salient point that was permitting fake Leonids to leak through the algorithms. I decided that the problem was that the false Leonids were all quite dim, so I put in a new requirement that a Leonid had to have a minimum brightness of 10,000. This cut way back on the false Leonids.
But another problem attracted my attention first: one Leonid was truncated: its first four frames, which were quite obvious to the eye, were missed by the algorithm. Much digging around revealed the problem: at the edges of the frame, where the spherical distortion is worst, the DX and DY values (that specify how far a Leonid should travel in one frame) are a bit off the mark. The Leonid in question was just over the edge of acceptability in one of the filters. So I widened the filter and ran another quick test; the algorithm seemed to do the job. I am now running a full test to see how many false positives have leaked through; if there are any, I’ll go through them to see exactly where they sneak through and fix that.
While I’m waiting for the run to complete (one run takes about two hours), I am contemplating one improvement to the algorithms. All Leonid flares are elongated in the direction of motion. I do not take this elongation into account in judging the likelihood that a flare is a Leonid; perhaps I should. The prime objection to this idea is that it will slow down the program. The critical algorithm here is a re-entrant routine that traces a flare by means of a walking-around process. Here’s how it works: we start with a typical Leonid flare, which looks like this:

Note how the Leonid flare is stretched out along a diagonal axis; this is characteristic of all Leonids. My algorithm differentiates between pixels that are of normal brightness and pixels that are significantly brighter than average. If you apply that algorithm to this image, you end up with something like this:
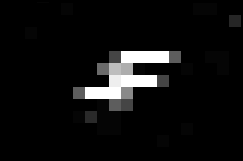
The black areas are treated as non-entities by the algorithm. It starts off in the upper left corner and sweeps from top to bottom, left to right, across the frame. The first pixel it will hit in this Leonid flare is the one furthest to the left. When it hits that pixel, it recognizes it as an atypically bright pixel, and swings into action.
The algorithm begins at pixel #0, which it marks as part of the flare. It then checks pixel #1, then #2, then #3, all the way to pixel #16. Each time it checks a pixel, it asks the question, “is this pixel significantly brighter than normal?” If so, then it does something that might confuse you: it shifts to pixel #1, marks it as part of the flare, and starts over, so that all the red numbers are shifted to the right by one pixel. It starts with its new pixel #1 (which was pixel #9 for the previous operation) and asks the same question. Each time it shifts position, it marks the new pixel as part of the flare and tests all the surrounding pixels (it has a scheme for remembering which pixels it has already been to, so that it doesn’t wander around forever). When it runs out of pixels to test, it back-steps to the previous pixel and resumes that pixel’s testing, until it has worked its way all the way back to the original pixel #0, at which point it decides that its work is done and all the marked pixels constitute the complete flare.
This process is called recursion and is probably confusing to you if you’re not a programmer. In a bid to help you understand, I show here the pixels in the order that they’re added to the flare:
So this flare has 22 pixels. I calculate its total brightness by summing the individual brightnesses of each of the 22 pixels. I calculate its “centroid” -- the precise location of its apparent center -- by averaging the positions of each of the pixels, weighted by their brightness. In order to obtain a measure of the elongation of the flare, I would have to save the locations and brightnesses of each of the pixels, and after I have calculated the centroid of the flare, sum up, for each of the pixels, the delta-X and delta-Y from that pixel to the centroid, weighted by its brightness. I could then compare these values with the DX, DY values that I use to predict the motion of the Leonid to see how much the flare looks like a Leonid.
But how do I factor this into my determination of whether to accept the Leonid? I measure “goodness of fit” as the square of the net errors. For example, it the flare is at location (fx, fy) and the flare is predicted to be at location (px, py), then the goodness of fit is:
goodness of fit = (fx-px)*(fx-px) + (fy-py)*(fy-py)
and I would measure the goodness of fit by comparing the net elongation of the flare (ex, ey) with the predicted elongation (dx, dy):
goodness of fit = (ex-dx)*(ex-dx) + (ey-dy)*(ey-dy)
But the problem is, how do I compare one with the other? Which is more important? Do I simply add the two goodnesses of fit together? That implies that elongation is just as important as position -- is that a good assumption? Remember, at the beginning and end of a Leonid’s trail, it’s very faint and shows just a few pixels, which won’t have much elongation. Will that cause my algorithms to truncate Leonids at the beginning and end?
I spent most of this afternoon and evening trying to figure out exactly how serious the problem with byeing was (byeing is my term for giving a free flare to a Leonid when it passes over a star). It turns out that real Leonids only need a single bye, but the fake Leonids always have more than one bye. So I adjusted the filter so that it blocked any Leonids with more than one bye. I’m running that test now and we’ll see if it doesn’t fix the problems.
