It’s been fifteen years now since my first job in the games business, and twenty years since I wrote my first computer game. We’ve come a long ways during that time, and it seems to me that there is much to be learned from the overall changes that have occurred during that time.
The most important overall change that we have seen during these fifteen years is a change of scale. No matter how you measure it, entertainment software in 1994 is bigger than software in 1979. But the manner in which it has grown bigger is itself interesting. I propose to discuss the changes in scale that we have seen and their implications for the design of entertainment software.
Scales of measurement
There are many scales by which we could measure the increase in the size of programs. The most obvious one is the size of the delivered code, including all support files. In 1979, this was 2K, primarily because commercial software was delivered in cartridge ROMs, which were expensive. By 1980, personal computers were well established and tape casettes had become the primary distribution medium. For these programs, the average program size leapt up to about 16K by 1981; however, larger sizes were impractical with tape casettes.
By 1982 disk drives were becoming common enough that software could be distributed on floppy disk; the higher capacities of floppy disks permitted another large increase in program size. Programs during this period were about 64K in size.
By 1985 the 16-bit machines were coming onto the scene with larger floppy disks; program sizes continued their growth, reaching several hundred K in size. For the next five years, programs continued to grow in size. By 1990 the average program had broken the 1 megabyte barrier in total size, and programs were often shipping in several diskettes. But then the demand for better graphics and sound arising from better displays and sound hardware led to a big jump in program sizes. Within two years, most programs were being compressed onto several floppy diskettes. Even before CD-ROM became widely available, program sizes were approaching 10 megabytes. With the advent of CD-ROM, program sizes exploded. Hundreds of megabytes were common. In the last year, the gigabyte limit has been broken.
A graph of this history is interesting:
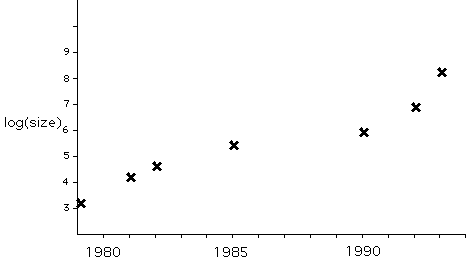
This graph uses a logarithmic scale for program size, so the 1994 value is nearly a million times larger than the 1979 value. This is an astounding development; in fifteen years program sizes have expanded by a factor of nearly a million!
Of course, I am using the term "program size" to refer to everything that goes into the software: the code and all the data files. We all know that code sizes have not increased very much; most of the growth has been in the ancillary data. Indeed, the primary cause of the huge leap since 1990 arises from the inclusion of video, which is very data-intensive.
Code Sizes
What about code sizes? How much have they changed? I spent a lot of time compiling data from a large number of programs, but in the end I could not come up with a statistically valid way of reducing the data to comparable formats. A great deal depends on the style of the program and the designer. For example, graphic adventures tend to have less code and more data. Flight simulators, at the other extreme, tend to have more code and less data. Empire Deluxe is almost all code; Myst is almost all data. The best I can do is reduce this unmanageable pile of data to some simplifications. In the early 1980s, programs were written in assembly language. In 1980, typical object code was about 10K in size, and grew to about 50K by 1985. By this time, designers were starting to use higher-level languages, primarily C, and object code sizes jumped up to about 100K. By 1990 typical object code was about 200K. Nowadays it is about 300K. The graph of this growth looks like this:
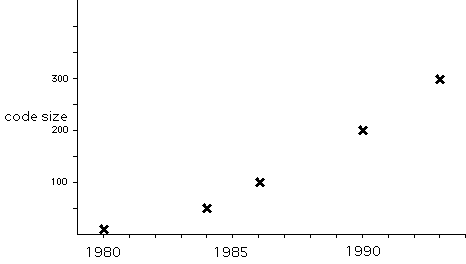
Note that, unlike the first graph, this graph uses a linear scale rather than a logarithmic scale. The growth in object code size has been much slower than the growth in overall program size.
There are two ways to look at this. One way is to compare the 30-fold growth in object code sizes with the million-fold growth in overall program sizes. This tempts us to condemn the programmers, who obviously must be lazy galoots indeed if they have managed to increase their output by "only" a factor of 30 when all the other contributors have increased their output so much more.
This is grossly unfair. We all know that program code is put together a byte at a time, by hand, while one can generate megabytes of video by running a video capture program with a camera. Indeed, when you recognize the handmade nature of object code, it is astounding that programmers have managed to increase their contribution by a factor of 30 in only fifteen years. I can’t think of any other field of economic endeavor in which output has increased so dramatically so quickly.
The 30-fold increase can be explained. First, it does not represent a 30-fold increase in productivity. Remember, we’re talking about the size of the object code. Back in the early 1980s, computer games were tossed together by single programmers in six to nine months. Nowadays, games are the product of large programming teams working for several years. I’d guess that the number of man-months (pace Frederick Brooks) that go into a game program has increased from 8 to perhaps 50. Right there we have a six-fold increase in labor input.
The other big change has been the use of high-level languages. There’s more going on here than merely the jump from assembly language to C. The fact is, our development tools have steadily improved with each passing year. The languages that we used in 1986 were bare-bones languages with few support tools; a considerable amount of routine labor was still required to actually build the final object code. Over the years we have gotten "make programs" and a wide array of other support programs that automate much of the overall process. This has considerably increased our productivity.
Another factor at work is that our higher-level tools produce fatter files. Back in the early days, we sweated every byte. Game programming was a smoke and mirrors exercise; could you create the illusion of a situation without expending the bytes required for its reality? Game programmers were masters of illusion, and players were willing to play along with the illusion. A good programmer knew all the tricks for moving bytes through the three registers of the 6502 as efficiently as possible. Over the years, though, it became less important to save a few dozen bytes here and there, and more important to get the code written quickly and bug-free. Programmers adopted a more liberal programming style, and their object code sizes ballooned accordingly. Our high-level languages yield object code that isn’t as tight or efficient as hand-coded assembly.
Bugs and Rats
One of the implications of this ever-larger code is that we are starting to experience a new class of programming problem. These are execution errors that arise from the great complexity of the design. We are tempted to refer to such execution errors as "bugs", but I think that these problems have reached a level of complexity that we need to think of them in different terms. I propose to call them "rats" because they’re bigger, smarter, and meaner than bugs. After all, a bug is easy to kill; you just step on it. But a rat is another story.
We know all the standard types of bugs that can infest our programs. Array index failures are among the simplest. We hand an array an index that goes out of the valid range of the array. Or we reference a dangling pointer that points to nowhere. Or we screw up a loop termination so that it hangs up. Particularly ugly are stack bugs, wherein we mess up the stack and the return structure of our subroutines is garbled; that bug always yields messy results.
But these are bugs, low-level programming mistakes. There’s a very different kind of error that arises from more complex considerations. Consider this case, for example: I designed Balance of the Planet with a system of 150 interconnected equations. It was a very complex system with lots of internal feedback .I found that, under certain circumstances, if the player steadily reduced the value of a critical intermediate value, and then shocked the system with a dramatic increase in another variable, the system would begin oscillating, and the oscillations would spontaneously increase in amplitude until a floating point error was generated.
This illustrates one of the differences between bugs and rats. A bug almost always arises from a single, identifiable error in the code. You can put your finger on the offending line and declare, "That was the mistake!" Then you need merely correct the mistake and the bug is fixed. But a rat is harder to pinpoint. The oscillatory behavior arose from the interaction of a variety of equations; which one was the "incorrect" equation? Taken in isolation, each equation is perfectly justifiable; the problem only becomes apparent when they interact. It would be just as fair to say that the problem arises from the absence of some corrective element.
Typically, an oscillation arises when two equations give each other the wrong kind of feedback. Let’s consider an example. Suppose that we’re modelling a classic predator/prey relationship, in which the population of the predators depends on the population of the prey. A simplified version might look like this:
Coyotes := RabbitMealSize * Rabbits;
Rabbits := FoodSupply - CoyotePredationRate * Coyotes;
Now suppose that RabbitMealSize = 1, FoodSupply = 100, and CoyotePredationRate = 2. Suppose further that we initialize Rabbits and Coyotes to 1. Here’s how the populations will change with each iteration:
Iteration Coyotes Rabbits
1 1 1
2 1 98
3 98 -96
4 -96 292
5 292 -484
6 -484 1068
I think you can see where this is going. Obviously, we have a rat in our system.
There are two common solutions to oscillation problems. The first is to include some negative feedback. This example is particularly useful, though, because its problem is that there is too much negative feedback. The most direct solution is to reduce the amount of negative feedback by adjusting the values of RabbitMealSize and/or CoyotePredationRate. If, for example, RabbitMealSize were reduced from 1.0 to 0.1, then the sequence of population values looks like this:
Iteration Coyotes Rabbits
1 1 1
2 0 100
3 10 80
4 8 84
5 8 84
6 8 84
This system of equations is stable, or "convergent". All we had to do was adjust the coefficients to stabilize it.
However, in most cases, the system of equations is more complex than this simple two-equation system. In such cases, the problem becomes one of determining which coefficients need to be adjusted. Now, if you’re very lucky, and all of your equations are linear, it’s actually possible to solve this problem analytically. That is, you can solve the system of linear equations and determine the coefficient values that will yield convergent results. However, my experience is that you never get well-behaved systems that can be tuned analytically. In the end, it all boils down to how well you can hand-tune the system.
Hand-tuning is definitely an art. The first trick is to identify the most volatile element in the system. That is, what equation jumps around the most? That’s the one you want to rope in. Next, identify the factor in the equation that is causing it to jump around. If it’s an additive factor, then you can constrain it with a multiplicative factor. Here’s an example. If the problem lies in the second term of our equation:
Rabbits := FoodSupply - CoyotePredationRate * Coyotes;
Then the solution is to reduce the value of CoyotePredationRate. That multiplier will dampen the oscillations in the system.
However, sometimes the problem lies in a multiplicative factor, something like our first equation:
Coyotes := RabbitMealSize * Rabbits;
If this is the equation you need to tame, the simplest solution is to slap a square root onto it:
Coyotes := SQRT( RabbitMealSize * Rabbits );
The square root function is a powerful tranquilizer for hyperactive equations. It preserves the concomitancy of the variation of the output with respect to the inputs, yet it dampens the wildest oscillations. The only objection to the use of the square root function is that it robs the system of responsiveness and personality. If you slap too many square roots onto your equations, you’ll end up with a bland system.
There are other functions you could use instead of square roots. You could use higher roots, such as the cube root or the fourth root. You could use logarithms. However, I discourage use of such functions for control purposes, because they constitute overkill, in my judgement. Where a square root provides a mild tranquilizer, a logarithm is a frontal lobotomy. If your system is so psychotic that it requires such extreme measures, it’s better to give it a major overhaul rather than resort to desperate measures. Moreover, the square root is a fast function to calculate; assembly language routines of only 100 lines or so can calculate a fast integer square root.
Testing For Rats
This is only the simplest of the approaches for stabilizing systems of equations. In many cases, the problem is primarily a matter of identifying the source of the problem. That is, many games have become so complex that certain situations that can generate abstruse rats occur rarely. Even more frustrating, conventional game-testing methods fail to catch the rat red-handed, and so the programmer denies the bug report that keeps cropping up every other week.
There are two deratting techniques that greatly help with such problems: black boxes and cybermonkeys. A black box is a routine that records critical state variables continuously, writing a file to the hard disk. A properly implemented black box makes it possible for the tester to halt the game at any time, copy the black box files to a floppy disk, and then hand the floppy disk to the programmer. The programmer can then use the black box files to restore the game to its exact state just before the failure occurred. The tester provides simple instructions which permit the programmer to replicate the failure from the restored game situation. This arrangement is far more reliable than the common shouting match that develops between programmers and testers, wherein the tester asserts the existence of a rat and the programmer dismisses it with the claim, "Can not be replicated." The tester writes up his procedure for replicating the rat, and then the tester tries it himself. If the tester can replicate the bug from the file, and the programmer denies it, then the tester can bring the programmer to his own computer and replicate the failure in front of the programmer.
I’m sure this sounds entirely too easy. Perhaps you’re telling yourself that a black box could not readily be implemented on your design. It’s true that some designs are more difficult to integrate black boxes into. The easiest designs are turn-sequenced games with clearly defined stopping points. All you do is store the game state at the stopping points. This involves nothing more than the standard save game routine that you would implement anyway. The only trick is that you set up a rotating save with, say, three steps in the rotation. In other words, you save Turn 1 to BlackBoxFile1, Turn 2 to BlackBoxFile2, Turn 3 to BlackBoxFile3, Turn 4 to BlackBoxFile1, Turn 5 to BlackBoxFile2, and so on.
Black boxes are most difficult to implement in games with lots of realtime play. The best that can be done is to set up the black box in RAM, and then copy it to the hard disk every 60 seconds. This can seriously interfere with gameplay, but testers aren’t there to have fun. Moreover, if the rat is so serious that it generates a crash, then replicating the problem can be difficult.
One aspect of black boxes is not difficult to deal with: isolating the black box code. You do this with a simple compiler flag. All through testing you leave the black box code in place. As you reach final beta testing, you turn off the compiler flag for the black box code and hope that no new bugs appear. If they do, you restore the black box code and try to isolate the problem.
Cybermonkeys
The second useful deratting technique is the cybermonkey. This is an automated testing routine that substitutes random inputs from a "cybermonkey" routine for the inputs normally provided by the human. Along with the cybermonkey, you set up a statistical sampling routine that keeps track of the performance of the system as a whole. You can set up breakpoints that will trap out ugly situations when they arise. Implemented properly, a cybermonkey can replicate months worth of human testing efforts in a matter of hours.
However, cybermonkeys are not always applicable. They are most useful in situations where the player has a small number of defined options at each point in the game, and these branchpoints occur rarely. The cybermonkey is least useful in games where the player has a great many options, most of which lead to failure. Such is the case with most skill and action games. If you imagine a three-year old playing Doom, I think you’ll see why a cybermonkey will be useless in such a situation.
Testing Defines Capability
Now, you might be shaking your head, muttering that these are interesting methods, but they are too restrictive; after all, you want to be able to do realtime games with lots of mouse input. You don’t want your designs to be constrained by the testing methodologies. But let me present the matter to you in a different fashion: the quality of the testing methodology limits the complexity of the final design. If you insist on designing a product that can only be tested by the time-honored manual methods, then practical considerations will force you to keep the design simple enough to be manually testable. If, on the other hand, you move the design in a direction that is easier to test, then you can afford to push the complexity to higher levels, confident that the bugs and rats will be flushed out and eliminated.
Programs have grown so large in the last few years that the ability to test them effectively is one of the limiting factors in the design. You can’t build what you can’t test. If you build it to be more easily testable, you can build it bigger.
