“The more I learn, the less I know.”
You don’t know jack. Neither do I. The world is far more complex than we realize. I have spent a lifetime learning about a huge range of topics: physics, mathematics, biology, linguistics, politics, economics, geology, evolution, computers, electronics, history, law, astronomy, psychology — it’s a long list. The more I have learned, the more insights I gain into the operation of reality, the more connections I see between all the different fields, and the more unified the universe seems to me.
Yet the expansion of my knowledge has only served to reveal just how miniscule my knowledge is. That is the inevitable consequence of the nature of knowledge. Your knowledge of reality falls into three classes:
1. What you know.
2. What you can see that you don’t know.
3. What you cannot see; you don’t even know that you can’t see it.
The knowledge you already possess provides you with your viewpoint of reality. From the perch of your knowledge, you can scan the horizon, taking in all the terrain that you don’t know yet. You can set out to explore that territory and expand your knowledge. But you cannot see beyond your horizon. You have no idea what — if anything — lies beyond the limits of your vision. You don’t know just how ignorant you are. Most people are so intellectuallly provincial that they think that their knowledge of reality is adequate to inform all their decisions.

Here are pictorial representations of the perception of reality of two different people. On the left is a more ignorant person. What he knows is yellow. The only things that he thinks he doesn’t know are the things that can be conceived in light of his limited understanding. They are represented by the blue boundary. Meanwhile, the vast terrain of truth outside his vision is simply lost upon him.
On the right is a less ignorant person. He knows more, so his appreciation of what he doesn’t know is greater than that of the more ignorant person. As he has accumulated more knowledge, his circle of appreciation has expanded and now he realizes that there is even more that he doesn’t know. Even then, however, his vision is still limited by the confines of his existing knowledge.
It gets worse: we don’t even know the scale of this representation. Let’s see those two circles in the context of the entirety of reality, which I will color pink. How do we know which of these two representations is more accurate?

I think that we can all agree that the representation on the right is closer to the truth. But how much further must we shrink the yellow circles to reach a proper representation?
A case in point: the orbit of the moon
To illustrate just how complicated reality can be, let’s take a simple case: the orbit of the moon. We all know that the moon orbits the earth, right? So we can write down a simple formula for the moon’s orbit:
The moon’s orbit has a radius of 385,000 km and a period of 27.322 days.
That was easy, wasn’t it? Oh, wait, the moon doesn’t orbit in a perfect circle. Its orbit is an ellipse. So we must add a correction; it’s called the eccentricity of the moon’s orbit, and it is 0.05488.
Oh, wait, there’s another problem: the moon’s orbit isn’t in the same plane as the earth’s equator. It’s orbit is inclined relative to the earth’s equator. That orbital inclination is 5.15º.
OK, now we have it down pat, right? Wrong, of course! The moon’s orbit is also tilted relative to the earth’s orbital plane, by about 1.5º.
I’m just getting warmed up. The moon is also affected by solar gravitation; half the time it is closer to the sun than the earth, and half the time it is further away. The difference amounts to about 0.5% of the net gravitational pull of the sun on the earth, so it definitely shifts the moon.
The other planets also affect the moon, but their effects are tiny. Even so, we can see those effects in the motion of the moon.
We’re not done yet. The moon is lopsided. It’s not a perfectly symmetrical sphere; the side facing us is slightly more massive than the back side. That causes the same side of the moon to always face the earth.
Oops, it’s not quite that simple — in fact, the moon nods slightly back and forth as it orbits the moon. Oh, and its axis of rotation is not quite perpendicular to the plane of its orbit, so it appears to yaw up and down a little.
I’ve left out the juiciest bit for last: the tides. The moon attracts the ocean water, which causes the tides, which are typically only a meter or two high. But the ocean water encounters some friction as it moves, which retards the tides. The highest tide always occurs some hours AFTER the moon is highest in the sky. That friction in turn causes the earth’s rotation to slow. Even more interesting, though, is that it pushes the moon away from the earth:
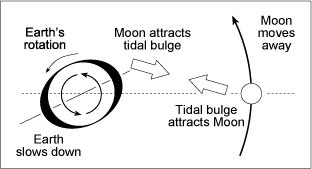
Another thing: the magnitude of the tidal effect depends on what part of the earth is facing the moon. There isn’t much tidal effect when the moon is over Europe and Africa, because those longitudes are mostly land. On the other hand, the tidal effect is really strong when the moon is over the Pacific, because there’s very little land.
There’s another tidal effect from the fact that the earth’s core is molten; it responds to the changes in lunar gravity in ways that ALSO effect the moon’s orbit.
While I was in grad school, one of my professors referred to an equation for the orbit of the moon that took into account all of these factors. It had something like 120 terms. I have been unable to find that equation on the Internet.
The moral of this story should be clear: even something so apparently simple and straightforward as the orbital motion of the moon turns out to be immensely complicated. Keep that in mind as you deal with more complicated questions.
