I built the original Gossip game way back in 1893 — no, it was 1983 — and thirty years later, in 2013, I decided to build a new version to demonstrate the most basic concepts of emotional interaction. The central verb in Gossip, and the most fundamental form of human interaction, is the “statement of affinity”: a declaration of how much one person likes or dislikes another person. Here I shall explain how the personality model in Gossip works. The mathematics used in the program deviated from the normal bounded number system in a few ways; after struggling to sort out the code, I decided to describe how Gossip would have worked if I had in fact programmed it using the full, true bounded number system.
Personality Model
The personality model uses only three intrinsic personality traits:
False_Honest: the degree to which an actor tells the truth
aFalse_Honest: the accordance value for False_Honest; that is, how readily the actor accords positive values of False_Honest to other actors. It could accurately be called “gullibility”.
Modest_Vain: the degree to which an actor values being flattered.
Surprisingly, the personality model does not use the intrinsic trait Bad_Good. Instead, it uses pBad_Good and cBad_Good, the perceived (2-dimensional) and circumferential (3-dimensional) values of Bad_Good.
The HistoryBook is a record of every statement made by anybody to anybody else. Actors consult the HistoryBook to review what they already know about what other actors have said to them.
Some terms
Speaker: the Actor who makes a statement.
Listener: the Actor to whom the statement is made.
Predicate: the Actor about whom the statement is made.
Value: how much the Speaker likes/dislikes Predicate, as measured by a BNumber.
Declaring pBad_Good
When Speaker declares their pBad_Good[Speaker][Predicate] value (that is, the pBad_Good value that Speaker holds for Predicate) to a listener, Listener will adjust three of their own values in response:
1. pFalse_Honest[Listener][Speaker]: how much Listener trusts Speaker
2. cBad_Good[Listener][Speaker][Predicate]: how much that Listener thinks that Speaker likes Predicate.
3. pBad_Good[Listener][Speaker]: Listener will like Speaker less if Speaker lies to Listener
In this lesson, I’ll address only the first item on this list. I will address the other two items in following pages.
The first task is to determine the degree to which Speaker’s statement disagrees with what Listener already knows. Listener consults the HistoryBook and compiles a list of all statements Listener has previously heard regarding Speaker’s pBad_Good towards Predicate. Listener than averages together all those statements to get the best overall estimate of pBad_Good[Speaker][Predicate].
What Listener Knows = sum of all Values of all statements about how Speaker feels about Predicate, divided by the number of such statements
In more computerish terms:
whatListenerKnows = Sum(Value(HistoryBook statement)) / number of HistoryBook statements
Suppose, for example, that Listener has already heard the following statements from other actors:
Sara told Fred that Joe likes Mary this much: 0.3.
Tom told Fred that Joe likes Mary this much: 0.1.
Lisa told Fred that Joe likes Mary this much: 0.5.
The average of all those Values is 0.3. Joe apparently likes Mary a bit.
Now suppose that:
Joe tells Fred that he likes Mary 0.5.
There’s a discrepancy here. The average value of previous statements is 0.3, but Joe now says that it’s really 0.5. This is suspicious, so Fred will suspect that Joe might be lying to him. So Fred will reduce his trust (pFalse_Honest[Fred][Joe]) by a small amount. We must calculate that reduction.
The discrepancy is, in simplest terms:
discrepancy = what Joe said about Mary minus what I already know about what Joe feels about Mary
or, in computerish terms:
discrepancy = 0.5 - 0.3 = 0.2
A small technical detail: we use the absolute value of the difference rather than the difference. Why? Suppose that Joe had told Fred that he likes Mary 0.1. Then we would have gotten this result:
discrepancy = 0.1 - 0.3 = -0.2
There’s a big difference between +0.2 and -0.2, but the actual discrepancy is the same in the two cases. So we use the absolute value, +0.2, to cancel out this little problem.
discrepancy = absolute value(0.5 - 0.3) = 0.2
But wait! There’s yet ANOTHER technical detail we must fix before we can proceed. What if:
Joe tells Fred that he likes Mary -0.8.
Then we’d get this result:
discrepancy = absolute value(-0.8 - 0.3) = 1.1
Heresy! Sacrilege! You can’t have a number outside the range from -1.0 to +1.0! The gods will surely reduce us to a smoking pile of ashes for such a sin. We’d better fix this.
Fortunately, there is a fix for this problem: another operator called BDifference. It’s just the bounded number version of subtraction. There’s also an operator called BSum; it’s the bounded number version of addition. Both of these operators insure that their results stay well inside the range from -1.0 to +1.0. For example, BSum(0.5, 0.5) is NOT 1.0; it’s 0.667. Therefore, we have this improved algorithm:
discrepancy = absolute value(BDifference(-0.8, 0.3)) = 0.816
Now that we’ve calculated the discrepancy, we can calculate the change in pFalse_Honest[Fred][Joe]. We’d probably want something looking like this:
pFalse_Honest[Fred][Joe] = blend(pFalse_Honest[Fred][Joe], -0.99, -discrepancy)
Where did that -0.99 come from? Well, remember, we’re always going to reduce Fred’s trust in Joe, so we must take it down, meaning closer to -1. So -1 should be the target we’re blending towards. However, we don’t ever use -1 because… well… er… in strict mathematical terms, -1 is an… um… evil number, and if you use it the gods will be angry with you and they will zot you with lightning someday. So we just use -0.99 instead. The gods don’t mind that at all.
Note also that we’re using the negative of discrepancy (-discrepancy) rather than the discrepancy itself. Why? Think about it: the bigger the discrepancy is, the further we want to go towards the lowest possible value (-0.99).
Suppose that Fred currently trusts Joe this much: pFalse_Honest[Fred][Joe] = 0.4 and that we have a discrepancy value of -0.2. Here’s what this situation would look like using our handy-dandy graph of the BNumber line:
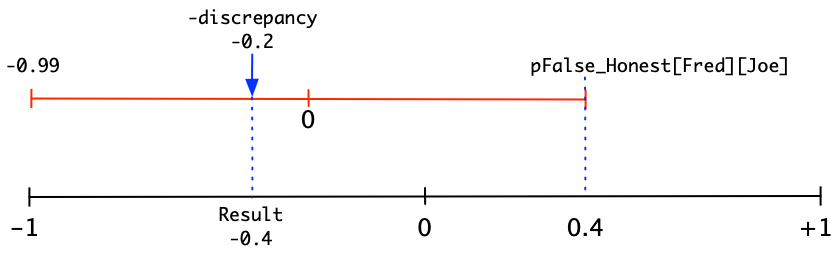
Remember, blend starts from the first parameter (pFalse_Honest[Fred][Joe]) and moves towards the second parameter (-0.99), going the distance proportional to -discrepancy. So the formula we’d use is:
Result = Blend(0.4, -0.99, -0.2) = -0.434
One More Problem
This might look good, but it has a terrible flaw. Suppose that
Joe tells Fred that he likes Mary 0.3.
Walk through the calculation. The discrepancy is 0.0; that is, Joe’s statement exactly matches Fred’s pre-existing knowledge. But look at the BNumber line: a -discrepancy of 0.0 will still lower Fred’s pFalse_Honest for Joe by a considerable amount, even though Joe appears to have been completely honest with Fred.
Uh-oh! The algorithm is wrong!
Well, not quite. The general idea of the algorithm is sound, but it obviously needs some adjustment. We want to insure that a discrepancy of 0.0 doesn’t change pFalse_Honest[Fred][Joe]. Which leads to another thought: if Joe is completely honest with Joe, shouldn’t pFalse_Honest[Fred][Joe] increase? Hmm…
Let’s start with one known fact: the upper red line should be centered over pFalse_Honest[Fred][Joe]. That is, the value of 0.0 in the upper red line should be directly over pFalse_Honest[Fred][Joe]. So we know that the BNumber graph should look something like this:

Except that this doesn’t work, either. We can’t have the high end of the red BNumber line poking out beyond the high end of the black BNumber line — that would give us an answer greater than 1.0, which is a serious no-no and will have the BNumber gods raining a storm of thunderbolts down upon us. So obviously we have to slide the red BNumber line to the left until its high end lines up with the high end of the black BNumber line. But that creates a new problem: where should the low end of the red BNumber line be? Should it be at the low end of the black BNumber line? No, that would be stupid, because then the red BNumber line would be lopsided.
Hmm… This is where we must do something that just isn’t done in the games industry:
It’s time to switch from nerd to artist!
We need to think about this problem from the artistic angle, not the nerdy mathematical angle. Let’s just ask ourselves some basic questions about the emotional response to lying. If somebody tells you the truth, how much will that increase your trust in them? If they lie, how much will that decrease your trust in them? My sense is that, if somebody tells me the truth, my trust in them will increase slightly, but if they lie to me, then my trust in them falls precipitously. But my response is lopsided. If they tell me something that’s a little bitty lie, I would just chalk it up to a mistake and wouldn’t change my trust in them. So here’s a short list of my assessment of human nature:
Big Lie: Big drop in trust
Moderate Lie: Small drop in trust
Little Lie: No drop in trust
Truth: Slight increase in trust
Now, presto-chango, it’s time to flip back to being a nerd. We’ll translate the art idea into nerdspeak:
Discrepancy > .5: pFalse_Honest[Fred][Joe] reduced considerably
(Discrepancy > .2) & (Discrepancy < .5): pFalse_Honest[Fred][Joe] reduced moderately
(Discrepancy > .1) & (Discrepancy < .2): pFalse_Honest[Fred][Joe] reduced slightly
Discrepancy < .1: pFalse_Honest[Fred][Joe] increased slightly
Where’d those numbers (.1, .2, and .5) come from? I just made them up; they’re not exact; they just serve to give the general idea.
So now we idea of the general scheme of the algorithm. Here’s how we proceed. The first step is to provide for the fact that little lies don’t cause a decrease in pFalse_Honest[Fred][Joe]. In other words, if somebody tells us something that’s ‘close enough’ to what we already think is the truth, then we’re likely to increase our trust in them. Here’s how to visualize it with the BNumber graph:
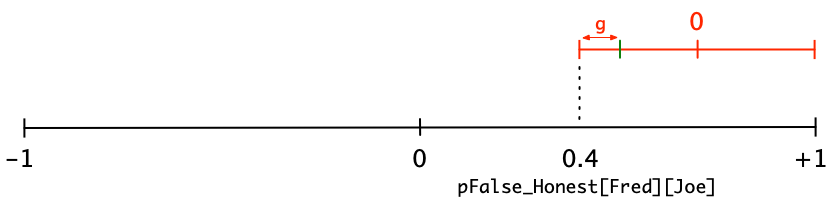
We put a little red BNumber line above the main black BNumber line. We set the low end of the red line to line up with the existing value of pFalse_Honest[Fred][Joe]. We set the high end to line up with the high end of the black line (except we make it 0.99 to keep the gods happy).Then we apply a Blend middle number I’ll call “g”. It represents the amount of grace that we give somebody for telling a small untruth. In this graph, the value of g is about -0.6. That’s my artistic guess as to how much grace we give somebody for telling a little lie. Here’s an exercise for you: if you think that people are less forgiving, then what value of g might you use? If you think that people are more forgiving, then what value of g might you use? Imagine sliding that green mark left or right along the right line. Where do you think the ideal position for that green mark is?
This new position marked by the little vertical green tick mark shows us the starting point for our next step. We know that, if Joe tells the truth, then discrepancy = 0, so we want to anchor the new line (it will be above the red line) with zero lined up with the blue tick mark.
But here we run into a new problem: we can’t line up the zero point of the new line with the blue tick mark, because then, well, almost any line will either be lopsided or it will have weirdo end points. We want something neat and clean. Now I’m going to pull a rabbit out of my hat: a new operator. So far, the only operator you have seen is Blend. But Blend works with BNumbers, and BNumbers always range from -1 to +1. Discrepancy doesn’t fit in: it runs from 0 to +1. It’s not really a BNumber! Instead, it’s what I call a “UNumber” (Unsigned Number). I call this rabbit-out-of-my-hat operator “UNumberToBNumber”. It converts a BNumber to a UNumber. (There’s also another operator called “BNumberToUNumber”, but we’ll skip that for now. And no, it doesn’t put the rabbit back in the hat.) The operator UNumberToBNumber merely stretches a UNumber to fit onto the full BNumber line, like this:
Now that we have UNumberToBNumber, we can fix our problem with discrepancy. Let’s return to the case in which discrepancy = 0.2. Then UNumberToBNumber(discrepancy) = -0.6 and our resulting BNumber graph looks like this:
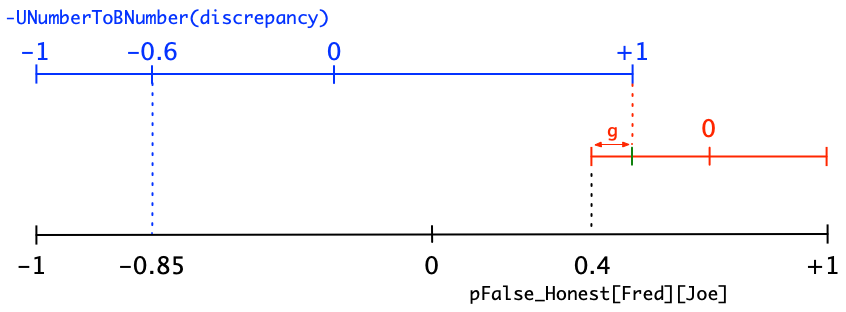
Woah! This is still way wrong!
Yep, a discrepancy of only 0.2 should not yield such a huge decline in trust. We need to dramatically scale back this process. We have just three numbers to play with:
1. The upper end of the blue BNumber line. Sorry, we can’t move that; it’s nailed down by the current value of pFalse_Honest[Fred][Joe].
2. The lower end of the blue BNumber line. Again, we can’t move that; if we put it anywhere else, then it would be impossible for a big liar who tells nothing but lies to get pFalse_Honest[anybody][Big Liar] down to -0.99. That’s just not acceptable.
3. That leaves just one number to play around with: UNumberToBNumber(discrepancy). If we make that smaller, then the value of -0.6 will become something more reasonable like, say, +0.4. So how do we scale back UNumberToBNumber(discrepancy)? That, it turns out, is easy; we just use Blend to push our result closer to the original value of pFalse_Honest[Fred][Joe]. Here’s a graphic of how we do it:
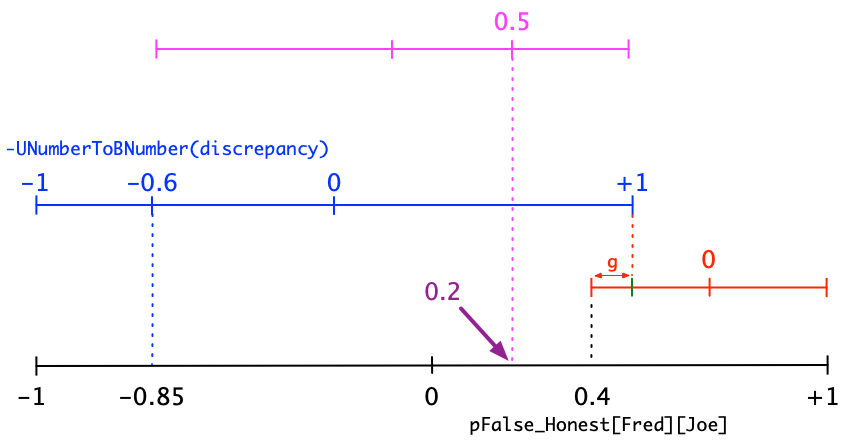
Don’t panic! Yes, it looks pretty hairy, but remember, we walked through every step of this process together, and every new line made sense. Now all we have to do is translate this geometric structure into the algegbraic form that we’ll use in the computer. We start at the highest level and work our way downward. I’ll use the same colors to connect each operator with its associated BNumber line:
GreenTickMark = Blend(pFalse_Honest[Fred][Joe], 0.99, g)
BlueTickMark = Blend(-0.99, GreenTickMark, -UNumberToBNumber(BDifference(Average, Claimed)))
pFalse_Honest[Fred][Joe] = Blend(BlueTickMark, GreenTickMark, 0.5)
Aren’t those just the prettiest equations you’ve ever seen?
Hello? Are you still there? Hello? Is anybody there? Hello?
