Interactive Storytelling Tools for Writers

Over the last few weeks I have carried out a fascinating text discussion with another game designer. He is brilliant and has a sterling track record. Our conversation eventually drifted over to interactive storytelling. Here we ran into trouble. When I mentioned the use of math, he rejected its utility for emotional interactivity on computers:

There are a lot of things wrong with this argument. First is its statement that “you can only create logical systems within it [math].” This statement assumes without justification that logic and emotion exist in two unconnected universes; that never the twain shall meet. One of our problems here is the gut-level disgust at the mechanization of modern culture. “I am human; do not fold, spindle, or mutilate!” The movie Koyaanisqatsi is one of the best expressions of the concept — and it is my favorite movie of all time.

But understanding is not dehumanization, and expressing truth is not compromised by the medium used to express that truth. Do you really think that the parts of human condition can be expressed by cutting open a cow, removing its intestines, and drying them? Seems ridiculous, doesn’t it? But until the last century, violin strings were made of catgut: the dried intestines of cattle. 

The same thing goes for other media. How can you use rocks to say anything emotional? 

It’s just a rock, fer crying out loud!

Or how about this: let’s cut down some trees, mash up the wood and mix it with water, then smear it onto a flat surface and dry it out, then take soot and mix it with some oil and water, and put the sooty water onto the mashed-up-dried wood. How could anybody possibly make art out of that mess? 

So let’s dispense with this silly notion that only “human” things can express the human condition. Mathematics is just another medium of expression, just like literature, cinema, painting, sculpture, or any of the other myriad wondrous things that humans have used to express themselves.

I wrote an essay on this concept a year or so ago: The Algorithm is the Message

Getting back to the conversation about interactive storytelling
I offered an explanation as to why math was crucial. Sadly, I failed to convince him. This distresses me for two reasons: first, it’s utterly wrong, and second, it’s a common belief. If a brilliant fellow like this can’t grasp the principle, what hope can I have for convincing people of the truth at any time in my life?

There is no question in my mind that people will eventually come around to this realization; the truth will out eventually. But how long will it take?

We already know the motivation for the rejection of math: people hate math. I don’t blame them; I hate it, too. Math, as I have often said, does to the mind what yoga does to the body. It’s unnatural. It’s unpleasant. It’s hard. But it’s central to interactive storytelling. No design failing to utilize math will ever produce anything remotely acceptable as interactive storytelling.

By now, you’re probably feeling some justified suspicion that I’m going too far, that I am too sure of myself. After all, whenever you have a disagreement between one person and the whole world, you really must question the sanity of that individual. But I know I’m right; ‘Here I stand; I can do no other’. So please indulge me to the extent of explaining my claim.

Object versus Process
The starting point is my observation about the distinctions between object and process. Here are some of the essays I have written on the subject over the years:

The operational approach to reality
http://www.erasmatazz.com/library/c839b0d2d6b6417787b1/what-is-the-essence-of.html

There’s also a lecture on the subject on Youtube:

The appropriate part starts at 6:00.

You can’t interact with object; you can interact only with process
You can’t interact with a book, a movie, music, a play, or any other form of data, because data is object. Here are some pieces on that:

http://www.erasmatazz.com/library/the-journal-of-computer/jcgd-volume-7/fundamentals-of-interactivi.html
http://comm6480rpi.blogspot.com/2008/09/interactivity-video-game-and-chris.html

Process is defined as algorithm
A process — any process — can be defined as an algorithm. Whether we’re talking about a manufacturing process, the process of an immune system reaction to disease, the process by which a person is hired, or the process by which two people fall in love, we are talking about something that can be defined by an algorithm. Obviously, some processes require more complicated algorithms than other processes. But you can always describe any process by stating an algorithm. 

You’re skeptical. You object that a process like falling in love is way too complicated to be expressed as a process. But this is merely a matter of abstraction. Here’s a highly simplified algorithm for falling in love:

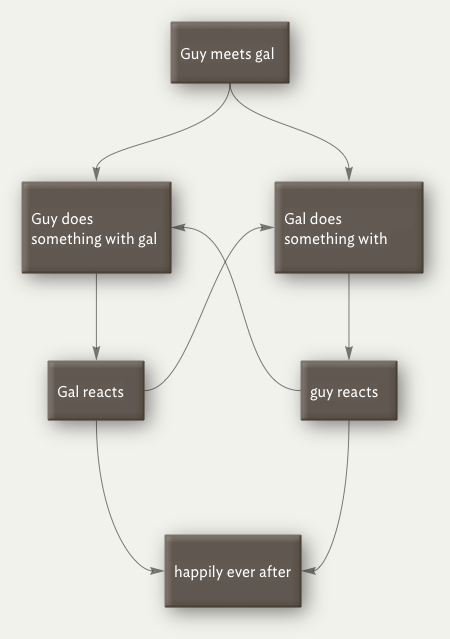
Sure, it’s ridiculously simplified. But you can easily imagine expanding each of those blocks into a bigger set of blocks, and expanding those to an even bigger set of blocks, and so on until you have huge, tangled mess. Sure, that tangled mess is really hard to figure out, but my point is that in principle we can write down an algorithm for every process.

Math is the language of algorithms
My next point is that the best way to describe an algorithm is through the language of mathematics. You could argue that a programming language is the best way to describe an algorithm, and I won’t argue with that, but I insist that math is an intrinsic part of programming languages. Intellectually speaking, the non-mathematical parts of most programs are none too demanding. Programming without math is rather like being an accountant. You must dot every i and cross every t, but you spend little time on grand ideas and most of your time dealing with stupid bugs and oddball issues about moving data around. Most programs don’t use the CPU much for processing; most programs spend most of their time shuttling data from one place to another.

Math is easily the most advanced way we have to express subtle ideas. Let me walk you through one of my standard examples. We have three characters in an interactive storyworld: Joe, Mary, and Tom. We desire to have algorithms for their emotional reactions to various situations. Suppose that one situation we wish to handle arises when one character says something emotionally significant to another. To be specific, suppose that Joe says something to Tom, and Mary witnesses the event. Now, Joe’s statement to Tom could be nice (e.g., “You’re looking good, Tom!”) or it could be nasty (e.g., “Are you still here, frogface?”) The challenge before us is to calculate Mary’s reaction to the event. Specifically, how does her affection for Joe change in response to his action? And how does her pre-existing affection for Tom affect this calculation?

Now, if this were a typical non-mathematical design, the calculation would be handled with boolean terms. We’d use a truth table looking like this:

This is ridiculous! People don’t base their entire relationship with others on a single event. In this kind of logic, romance looks like this:

Mary_Likes_Joe = FALSE

Mary_Likes_Joe = TRUE

Sorry, folks, but the world isn’t this simple. Mary’s affection for Joe is a number, not a flag. It varies from tiny values to large values. Joe’s actions change her affection for him by tiny amounts. There isn’t any single thing he can do that will get her into bed with him. It takes a lot of interaction for love to develop. The effects of those many small steps cannot be handled by simplistic black-and-white determinations. Instead, we need a number to reflect her affection for him. And how can you work with numbers without using mathematics?

I doubt that many people will understand this for another few decades.

Postscript, November 6th
I received a nice email presenting some arguments that led me to realized that I have failed in this essay to explain a crucial point about the use of math in software design. 

Math is always applied to problems that can be rigorously solved. The application of math to a problem requires a long, convoluted logical process that starts with first principles and leads inevitably to a provable numeric conclusion. 

Most people think that this is the ONLY way to apply math, and if that were true, then I would never suggest that math be used for artistic expression. The key point that I neglected to make is that math can also be used for non-logical problems. 

First-order approximation
Let’s use the example above to illustrate the concept. I never showed how I would use math to address the problem of how Mary reacts to Joe’s comment. Without explaining why, I will offer this first-order solution:

Change_In_Mary’s_Affection_For_Joe = Mary’s_Affection_For_Tom * Nice_Nasty_Of_Joe’s_Comment

We simply multiply the two numbers together, using a number system in which 0 represents neutrality, a positive number represents a “good” value, and a negative number represents a “bad” value, and the magnitude of the value expresses just how good or bad that item is. 

Second-order approximation
OK, that’s a nice solution, but it is certainly not definitive. I can see a number of ways to improve it. The first is that the above equation overstates the magnitude of Mary’s reaction. The kinds of numbers going into the calculation are numbers between -1.00 and +1.00, with 0.00 representing neutrality. If the two input figures are, say, 0.2 and -0.4, then the change in Mary’s affection will be -0.08. That seems rather high to me for such low input values (Mary likes Tom just a little, and Joe’s insult was only mildly negative.)

So I need to scale down the impact of this even on Mary’s affection for Joe. I can do this by simply dividing the right side by some number. To simplify matters, I’m going to generalize the variable names. The little triangle at the beginning is a standard math symbol for “the change in”.

∆ Affection[Mary, Joe] = 0.10 *(Affection[Mary, Tom] * Nice_Nasty[event]

So I multiply the earlier equation by 0.10, reducing the result from 0.08 to 0.008.

“But wait!” you object. “Where did that 0.10 come from?” 

Answer: I just made it up. It came from my gut. More precisely, it came from my personal assessment of human behavior. This is where I express myself artistically. Another person might differ with me, declaring that this is too strong a reduction. I don’t need to argue with that person; art is entirely subjective. Let her use 0.20 instead of 0.10 when she designs her own piece. Or another person, certain that people don’t react strongly to verbal behavior, might use 0.05 instead of 0.10. There’s no arguing over the number; it’s art.

“But wait!” you say again. “How do you decide on a number?”

Answer: I have a feel for how numbers work. Every artist must have a feeling for their medium. Painters absolutely, positively need a feeling for light and how the eye works. Musicians have a feel for sound and its effects on human emotion. Poets have a feeling for language. There’s nothing any different about having a feel for numbers and math. It’s just one more form of art. I enjoy music, but I could never actually play it; I just don’t have the feel. 

Passing a math course in school doesn’t mean that you can use math as a medium of artistic expression. You have to use numbers for years, developing experience in how numbers work, how equations can be adjusted, why you use multiplication in some cases and addition in others. Sure, it takes time to develop. Isn’t that true of any artistic medium?

Third-order approximation
Let’s go a step further. Let’s directly address the argument over whether the multiplier should be 0.05, or 0.10, or 0.20. What if we create a new variable called “Volatility”, representing the magnitude of a person’s reaction to an event. If Mary is highly volatile, reacting to events with a lot of emotion, then she’ll have a high value of Volatility, like 0.20. If, on the other hand, she doesn’t get upset by things, then she has a low value of Volatility, like 0.05. 

So we modify our equation to look like this:

∆ Affection[Mary, Joe] = Volatility[Mary] *(Affection[Mary, Tom] * Nice_Nasty[event]

The advantage of this formula is that it can be used for any combination of characters:

∆ Affection[Jane, Bill] = Volatility[Jane] *(Affection[Jane, Fred] * Nice_Nasty[event]

Now the equation can be used in lots of different situations.

We could continue this process with a fourth-order approximation, a fifth-order approximation, and so on. We can go as far as our artistic sensibility demands.

“But wait!”, you say for the third time. “Mustn’t I take this all the way to perfection? Don’t I have to go to the 100th-order approximation, or it won’t be true? 

If so, you have a lot to learn about art! Art does not capture the entirety of truth; in fact, good art strips away everything irrelevant to the artistic message to concentrate the audience’s mind on the message. Here’s an example I have used many times before. Let’s compare stills from a movie and a game. First, the movie, Brave. 

You can easily see the emotions expressed on these faces. Now, the game:

The upper faces are not accurate; they are cartoon faces, not real faces. By contrast, the faces in the game are much more realistic. But they’re DEAD! There’s no emotion in them, no artistic oomph. The artists for the upper image concentrated on conveying an artistic message in the emotions they show. The artists for the lower image achieved realism at the cost of art. 

“But wait!” (this is getting repetitious) “Couldn’t the artists in the lower case simply put emotional expression onto those faces to get both realism and emotion?” 

Nope. If you look carefully, you’ll see that the upper faces are inconsistent; different features of the face are larger or smaller in different frames. For example, the mouth for “mock sympathy” and “assertive” is smaller than the mouth for  “satisfaction at success” and “defiant”. That’s the artist’s interpretation of the facial expression. The eyes in “proud” are smaller than the eyes in “sarcasm”. We see an even better example of this in another movie:

This face is way, way inaccurate. That’s deliberate. The artist has made the mouth far too big; the eyes bulge more than is physically possible. This is true art, in the sense that it communicates emotion. An artist exaggerates some elements of the work and minimizes other aspects, all to communicate better. 

Conclusion
You don’t need to get any mathematical expression perfect; you need only make it good enough to serve the purpose of your work. If you’re going to build a storyworld about sex, you don’t need to include anything about toiletry, and certainly few details about meals other than their romantic character. You should suppress all that stuff with simple algorithms. On the other hand, you want to include detailed algorithms for seduction and lust. Even then, it doesn’t have to be perfect; just good enough to make your point.