Goal of this Appendix
My goal in this appendix is to explain in simple terms exactly how it is that a mess of silicon can do all the wonderful things that computers can do. This is certainly a tall order, but not an impossible one. If you have followed me this far, you should have no problems understanding this appendix. However, while the concepts themselves are simple, they do tend to pile one on top of one another in a rather intimidating heap. If you pay attention and bear with me, we’ll pick this heap apart. I assure you, the result — the knowledge that even the mighty computer is within your mental reach — will be worth the mental exertion.
My fundamental strategy in this appendix will be a process of agglomeration. I’ll start with the simplest building blocks and use them to assemble bigger building blocks. These bigger blocks will then form the basis for the next, even bigger group of building blocks. At each stage of the game, once you understand how the building block is put together, you forget the internal details and just treat it as a black box whose properties you have already figured out. Its kind of like going from atoms to molecules to cells to people to societies. Leaping from atoms to societies is a mind-boggling endeavor, but if you take it in steps, it really can make sense. Let’s begin.
Level One: Transistors
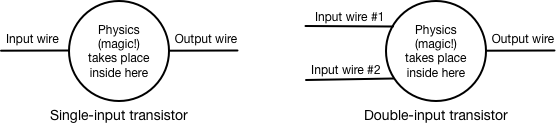
The atoms of a computer are transistors. A typical personal computer will have millions of these little devices inside its chips. What they do is very simple, but how they do it involves a great deal of tricky physics, which I explain in another appendix. A transistor controls the flow of electricity by controlling electrons. The big trick is its ability to control the flow of many electrons with just a few electrons. Crudely speaking, it uses a few moving electrons to stampede many more electrons. The result is like a switch that is controlled by electricity instead of a finger. You can use the presence or absence of electricity in one wire to turn on or turn off electricity in another wire.
Three special properties of the transistor make it possible to build computers out of transistors. The first is that we can run it either all the way on or all the way off, and treat those two states as numbers. If the transistor is on, we say that it means "1"; if it is off, we say that it means "0". All the 1s and 0s inside a computer are just represented by transistors that are turned on or off. We can extend the idea to the wires inside a computer. If a wire has electricity on it (meaning that a transistor connected to it has turned on), then the wire represents a "1"; if the wire has no electricity, it represents a "0". It’s not as if there are tiny little 1s and 0s printed on the wires; it’s a code. Electricity means 1, no electricity means 0. This gives us the ability to manipulate numbers (i.e., to compute) by manipulating electricity.
The second special property of the transistor that makes computers possible involves a special type of transistor that can have not one but two independent controlling wires. Earlier, I said that a transistor is like a switch that is controlled by electricity instead of a finger. Well, it is possible to make a transistor that uses two finger-wires instead of just one. It’s rather like the double light switches in long hallways in some houses — either one will turn on the light.
The third special property of transistors is their ability to invert the relationship between input and output. Normally, we think of the transistor as creating a direct relationship between the input wire and the output wire: if there is electricity on the input wire, it turns on the output wire, and if there is no electricity on the input wire, then it turns off the output wire. It is also possible to make transistors reverse this relationship, so that electricity on the input wire will yield no electricity on the output wire, and no electricity on the input wire will yield electricity on the output wire.
Let’s summarize what we’ve got on transistors with some simple diagrams:
Level Two: Gates (Assemblies of Transistors)
We can use transistors as the building blocks for the next level in our hierarchy: the gate. A gate is an electronic circuit that accepts one or more inputs and produces a single output that is a logical function of the inputs. In simple terms, you plug wires into it and it has one wire coming out of it. Whether or not the output wire will have electricity on it depends on the electricity on the input wires and the rule that the gate uses. The first type of gate is called an "AND” gate, and it’s really just the double-input transistor shown above. However, now that we’re treating it as a logical unit rather than an electrical unit, we have a new symbol for it:

The rule for the AND gate is simple: if the first input is a 1 AND the second input is also a 1, then the output will be a 1. Otherwise, it will be a 0. This is just like the Boolean AND function you use in programming; in fact, this is the electronic circuit that the computer uses to make that program work.
The second type of gate is called the "OR" gate, and the diagram we use for it looks like this:

The rule for the OR gate is also simple: if the first input is a 1 OR the second input is a 1, then the output will be a 1. Otherwise, it will be a 0. Again, this is just like the OR Boolean function you met in programming and is the hardware source of the software capability.
The third simple gate is hardly a gate at all: it is a simple inverter, and it is diagrammed like so:

The inverter simply takes the input and inverts it, so that a 1 becomes a 0 and vice versa. This little guy is handy for all sorts of jobs.
These different gates are all assembled out of various combinations of transistors. The NOT gate is really just a single transistor; the AND gate is just a two-input transistor. The OR-gate uses a combination of several transistors and inverters. We can also put together transistors with a NOT-gate at the end to make a NAND gate (NOT - AND: the output is false if both inputs are true, otherwise the output is true. We can do the same thing with a NOR gate.
Level Three: Decoders, Latches, Adders (Assemblies of gates)
We can use the gates we have just built to create even more elaborate devices. The first new assembly is called a decoder. Its purpose is to electronically convert a numeric reference to a specific one. Instead of talking about "the third one", we can use a decoder to talk about "that one". Suppose, for example, that we have a wire. It can carry a 1 or a 0. Thus, one wire can represent one of two choices. We could, for example, use it to select one of two light switches that we might want to turn on. In other words, if the wire has a 0 on it, then we want to turn on light #0, and if it has a 1 on it, then we want to turn on light #1. However, there’s a problem: the wire by itself can’t turn on the right switch. If we hook it up directly to a light, it will turn the light on when we have a 1 on it, and turn it off when we have a 0 on it. We need a decoder. A decoder for this job might look like this:

If you put a 1 into this decoder, Ouput #0 will have a 1 on it and Output #1 will all have 0. If you put a 0 into this decoder, then Output #0 will get a 1 and Output #1 will get a 0. In short, a decoder translates "Gimme number x" into "Gimme that one".
The next doodad we will build is called a latch. We build this one from NOR gates. “NOR" means "Not OR"; it is just an OR gate whose output is inverted. In other words, we take a plain old OR gate and stick an inverter on its output. We indicate this by putting a little circle on the end of the OR gate; that makes it a NOR gate. The rule for a NOR gate is, loosely speaking, “Neither one input nor the other input”. Specifically, if Input #0 is a 0, AND Input #1 is a 0, then the output will be a 1; otherwise, the output will be a 0. So, here is a latch:
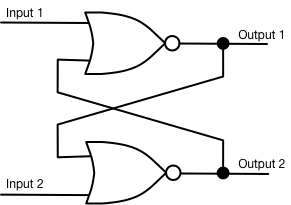
(A fine point: where the lines cross, they are not considered to be connected unless there is a dot marking the crossing point. Thus, there is no connection between the diagonally crossing wires in the center. There are two connections marked by two black dots.)
Let’s walk through the operation of this little circuit. Remember this simple rule: a NOR gate has an output of 1 only if both of its inputs are 0s. Let’s just suppose that when we first look at our latch circuit, it’s in this setting:
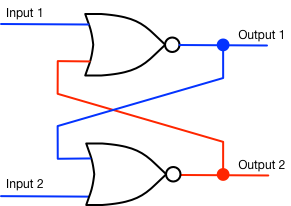
This is a stable situation: the upper NOR gate outputs a 0 because the input from the second NOR gate is a 1. But the lower NOR gate has two blue inputs (both are 0), so its output is a 1 (red). Pretty simple so far. But now let’s suppose that we put voltage on Input 2, changing it from blue to red. Three steps take place in extremely rapid succession:
Now, here’s the good part: if we stop putting voltage on Input 2 (we let it go to 0), then the latch looks like this:
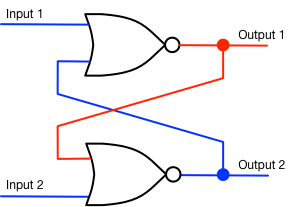
Nothing changes because the lower NOR-gate still has one red input. The circuit remembers what happened to it! Now an exercise for you: suppose that we changed Input 1 to red. How would the circuit change? Then suppose that we let it drop back down to blue — what would happen?
You now understand how computer memory works. (Actually, most of what you think of as memory operates on a different principle, but inside the CPU, this circuit is how memories are stored.)
The last device we will assemble is called an adder. It is not a snake, but a circuit that will add two numbers together. In this case, we are going to keep it real simple: we are going to add two single-bit numbers. In other words, this circuit will be able to calculate just four possible additions:
0+0=0
0+1=1
1+0=1
1+1=10
That last addition may throw you; since when did one plus one equal ten? Remember, we are working in binary numbers here, and binary 10 is just decimal 2, so the equation really does work. Here’s what the adder looks like:

The table on the right is called a truth table, and it is a quick way to double-check the operation of a circuit. It shows the result coming out of the adder for each of the four possible input configurations. It really does add!
We now have devices that can select, remember, and add. Time for the next step.
Level Four: Breadth
We are now going to expand the circuits we have to make them more practical with real numbers. The above circuits are all single-bit circuits; each one can handle only a single bit of information. The decoder can decode just one wire, selecting one of only two possible options. The latch can remember only one bit, a single 1 or 0. And the adder can only add two single-bit numbers. These devices are almost useless. Who wants to add 1 to 0 all day long? Who needs to remember just a single 1 or 0?
The big trick we are going to pull is embarassingly simple. We are going to gang each of these devices up in parallel with a bunch of its brothers. Lo and behold, they will suddenly be useful! Let’s start with the latch, for it’s the easiest one to understand. Here’s a diagram:
This is nothing more than eight separate latches sitting side by side. Behold one byte of memory. Your computer probably has about 8 billion of these. You can store an eight-bit number in here. That’s enough to denote one character of simple text, or an integer between 0 and 255. As you can see, one little latch may not do much, but when it gangs up with seven siblings, it suddenly becomes a worthwhile bit of silicon.
I won’t show you how we broaded decoders and adders; those circuilts are more complicated. However, I hope you agree that the example above demonstrates the principle that we can take one-bit circuits and gang them together to get 8-bit circuits or even wider. Most computers these days work with 64 bits; that’s a lot bigger but the principle is the same.
Level Five: Assembling RAM
Now we are ready to explain our first major computer component: the computer’s RAM. The computer must be able to access all of the bytes in its RAM. If it has 8 gigabytes of RAM, that’s 8 billion bytes, or 64 billion bits. If the computer wants to access every one of those 64 billion bits of memory, it would need 64 billion tiny wires, one going to each bit, right? That’s ridiculous! There’s gotta be a better way.
There is, but it’s a little harder to understand. It’s called a bus. A bus is a bundle of wires that everyone shares. Think of it as like a hallway on a floor of a busy hotel; many different guests use the hall, but they all use it at different times. A computer bus has a simple rule: only one signal can use the bus at any given instant. Every computer has three buses: the address bus, the data bus, and the control bus.
The address bus is the easiest to understand. It’s a bundle of 64 wires; together, they can address 20 zettabytes of memory. That’s 20 sextillion bytes. In truth, some of the wires aren’t actually connected to anything, because at the current retail price of $10 per gigabyte, a computer would need about $100 billion worth of RAM to need to use the address bus. So computer manufacturers save a few bucks by not using all those address bus wires.
A quick digression about the technical term word. In computers, a word is a bundle of bits that are taken as a single chunk. When I was just a whippersnapper, building my own computer, that computer had an 8-bit word. Nowadays our computers use 64-bit words. So where my old computer was a little guppy taking one little byte at a time, modern computers are huge sharks taking much bigger bites of data.
Each 64-bit word of RAM has its own unique number, called an address. The first word is called word #0, the next one is word #1, then word #2, #3, and so forth until we reach the last word, #1 billion in our example. This is where the decoder I described above comes in. Remember, a decoder translates a binary number into a “pick this one” signal. The CPU puts a binary number onto the address bus; that binary number goes to the RAM in the computer, and that decoder decodes that binary number into a “pick this one” signal — which will select a single word out of all those billion words.
Once a word has been selected, the RAM puts the word onto the second bus, called the data bus. The data bus carries that word from the RAM to the CPU chip, which then uses the word in whatever calculation it’s working on. When it has digested that word, it puts a new address on the address bus to get another word from memory.
The control bus is just for housekeeping. It acts as the regulator, telling memory when an address is ready to be used, and turning over control of the data bus to either the CPU (so that it can write a word into memory) or the memory (so that the CPU can read the word from memory.) It also carries the all-important clock signal. The clock is just a simple circuit that ticks and tocks. When it ticks, it puts a 1 onto its special wire. When it tocks, it puts a 0 onto that special wire. Everybody inside the computer monitors that clock signal. It’s like the metronome that regulates the timing of music, only inside the computer, it regulates the timing of the various events taking place. Here’s a simplified timing diagram to give you an idea of how this works:
Tick: CPU puts an address onto the address bus
Tock: RAM reads the address and selects the appropriate word
Tick: RAM puts the word onto the data bus and CPU reads it
Tock: CPU processes that word
Tick: CPU puts another address onto the address bus
…and so on. Obviously, the speed that the computer runs at depends on the clock. A faster clock means a faster computer. Current computers have clocks running at about 3 GHz — three billion tick-tocks per second. To give you an idea of just how fast that is, consider this: in one tick-tock of such a clock, a beam of light could travel about four inches.
Level Six: The Central Processing Unit (CPU)
Our next creation will be the heart of the computer: the CPU. This is the unit that actually crunches the numbers, runs the programs, and loops the loops. In this highly simplified and imaginary computer, we will have but four parts: the ALU, the registers, the address controller, and the instruction decoder.
We shall take up the ALU first. ALU is an acronym for "Arithmetic and Logic Unit". The ALU is a rather like one of those all-purpose handy-dandy kitchen utensils that slices, dices, and shreds, only it does its work on words rather than morsels. Instead of a collection of blades in various shapes and sizes, the ALU contains all of the number-crunching tools to carry out addition, subtraction, multiplication, division, ANDing, ORing, and so on.
The registers are another simple part of the CPU. These are simply words of RAM inside the CPU that can be used as quick storage of intermediate results. The relationship between register-RAM and regular RAM is rather like the relationship between your kitchen counter and the kitchen cabinets. You keep your ingredients in the cabinets and the refrigerator, but when it comes time to work with them, you move the various ingredients out of the cabinets and onto the kitchen counter where you work with them. The countertop can’t hold a lot of ingredients, but it’s much easier working on the countertop than. Almost all programs follow a very simple strategy: bring some words out of RAM into the registers; crunch them up; spit out the results back into RAM.
The address controller is rather simple: it’s just a register that contains the address of memory that the CPU wants to read or write into. When the CPU wants access to a word in memory, it sets the address controller to that address.
Here’s where we get into a special trick that is fundamental to all computers: the alternation between program and data. So far, I’ve described the computer as if all it does is retrieve data from memory, process that data, and then write the results of its processing into other places in memory. But I’ve left out a crucial behind-the-scenes activity.
Computers are controlled by programs, right? And where do you think that those programs are stored? Right: in memory. So as the computer steps through the program, it must retrieve individual program steps from memory. So here’s what the process mentioned above actually looks like:
Tick: CPU puts an address onto the address bus
Tock: RAM reads the address and selects the appropriate word
Tick: RAM puts the word onto the data bus and CPU reads it
Tock: CPU puts the address of the next instruction word onto the address bus
Tick: RAM puts the instruction word onto the data bus
Tock: CPU loads the instruction processor into its instruction decoder
Tick: the instruction decoder directs the CPU what its next step should be
Tock: CPU processes the data according to the instruction
Tick: CPU puts another address onto the address bus
In other words, the CPU alternates between processing the data itself and retrieving the program instructions that tell it how to process that data. In its simplest form, the CPU simply alternates between retrieving data, retrieving an instruction, processing the data according to that instruction, and retrieving the next instruction. Sometimes, however, the instruction can be pretty complicated, involving a number of different steps.
Now we are ready to tackle the inner sanctum of the CPU: the instruction decoder. This is the module that actually translates instructions into action. It is the heart and soul of the entire computer, the most necessary of all the necessary components, the essence of the computer. It is based on nothing more than the simple decoder, with a number of intricacies added. There are two broad types of information conveyed in a typical microcomputer instruction: what to do and who to do it to.
The “what to do” part is easy to understand. This boils down to just two basic types of commands: move information or crunch information. Moving information is just a matter of taking a word from one place and storing a copy someplace else. Depending on the complexity of the processor, you might have any number of combinations here. You could move a word from one register to another register, from a register to RAM, or from RAM to a register. The crunching part just tells the CPU to use the ALU to crunch two words.
You may wonder, what does an instruction word look like? It’s just a number. Recall from the end of the chapter “From Data to Information” that a number can represent a program instruction. You might wonder, how do you get from a number like “174” to “load a number from memory”? That translation is the job of the instruction decoder. It must use that number to activate the appropriate circuits inside the CPU to execute the instruction.
All this is based on a fancy decoder circuit. The bits of the instruction go to the decoder. If they indicate a crunching operation, the decoder activates the ALU, sending it the proper code to activate the desired circuitry inside the ALU. If the instruction indicates a move operation, then the decoder will select the proper registers or RAM locations and send the proper signal to the Read/Write line on the control bus to indicate the direction of the move operation.
The next part of the instruction specifies the object of the command; normally this is a register or RAM-location. For example, if we have a move instruction, we must specify the source and destination register or RAM location. With a typical computer, this is done with an additional word that follows the main instruction word. Thus, the command would consist of two words. The first word says “Load this register with the word in the RAM location whose address follows”. The second word give the 16-bit address of the RAM location. The instruction decoder, when it receives the first word, opens up a digital pathway that will send the next word straight into the address controller; then it activates the address controller, which in turn fetches the word from the address it holds.
In essence, then, the instruction decoder translates numeric instructions into action by using decoders that activate different sections of the CPU. Some decoders might open up pathways in the CPU to ship bytes around to different locations; some might activate the ALU; some might activate multi-step sequences. In a real computer, it might be very complex, but it is certainly not magic.
And that is how computers work.
