Like any good morality tale, there was a flaw in life’s march to perfection. The early nervous system could integrate patterns distributed across multiple sensory dimensions, but it couldn’t integrate patterns distributed across time. Your basic Triassic dinosaur could easily recognize the ominous sound of heavy footfalls, but he couldn’t figure out that increasing amplitude of footfalls meant approaching danger, and decreasing amplitude of footfalls meant receding danger. Obviously, such an ability would be most conducive to survival, but the basic layout of nervous systems didn’t handle this problem very well.
Let’s examine closely the problem of recognizing the difference between approaching footfalls and receding footfalls. Here’s the crucial problem: in order to know that one footfall came after another footfall, your neurons have to have memory. That might sound easy, but in fact, getting neurons to remember things is really difficult. In our last exciting chapter, where I explained how neurons deduce that something is moving, I used a simple trick: I had the neural circuitry “remember” the first appearance of the object by routing the signal through a slow neuron. That “remembered” the event just long enough to permit it to be combined with the second appearance of the object. But that works only when the two events are very close together in time. If you want to remember something that happened, say, one second earlier (such as a footfall), then you can’t use slow neurons; you need something better. Here’s that something:
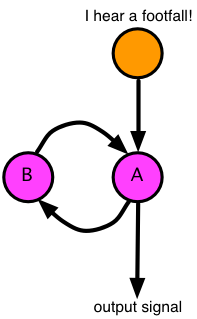
In this circuit, the orange neuron triggers when the creature hears a footfall; this causes neuron A to fire; neuron A sends out an output signal and it also sends out a signal to neuron B. Then neuron A turns back off. Meanwhile, neuron B receives the signal from A and responds by firing, sending a signal to neuron A. This causes A to trigger, and we create an “infinite loop” in which A and B trigger each other forever. The good news is that this simple little circuit remembers the initial trigger. The bad news is that it never forgets, and it keeps sending its output over and over again. So we need to add a way to make this circuit forget. That’s not difficult; here’s the solution:
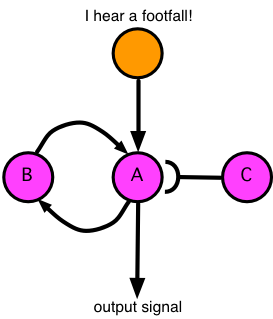
You may recall that the half-circle at the end of a line means “inhibition” -- the signal from neuron C will inhibit neuron A, preventing it from triggering, which will cause it to forget. Thus, when we’re done using the output signal, we just trigger neuron C and it shuts down this little memory cell. But we’re still far from a solution to our problem of remembering the footfalls; we want to forget the first footfall after enough time has passed that we figure that there aren’t any more footfalls coming. Let’s use 3 seconds as our limit; if another footfall isn’t heard within 3 seconds of the first, then we can forget the first footfall. Here’s how that’s done:
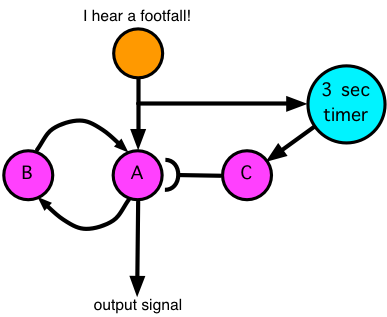
The initial trigger starts the 3-second timer, which signals neuron C after 3 seconds, which shuts down the memory circuit. How does the 3 second timer work? It’s something like the memory circuit, except that it has a counting system that tells it how many times it has looped the loop, and it knows to fire when it has completed a specified number of loops. So now let’s add some more circuity to handle a second step:
Here’s how it works: when the creature hears a footfall, the orange neuron triggers and sends a strong signal to yellow neuron #1 and a weak signal to yellow neuron #2. The signal is strong enough to trigger yellow neuron #1, but not strong enough to trigger yellow neuron #2. Circuit #1 on the left locks in and remembers the first footfall for three seconds. If no more footfalls come, then it forgets it. But if a second footfall is heard while circuit #1 is active, then green neuron number 1 will be sending a weak signal to yellow neuron #2 at the same time that the orange neuron is sending a weak signal to yellow neuron #2. Those two weak signals added together are strong enough to trigger circuit #2, which now remembers the second footfall for three seconds. Now all we do is add a third circuit to this mess:
And here we have a schematic for a neural circuit that can detect three footfalls in sequence. You might observe that it takes a LOT more neurons for this kind of work than it takes for the simple pattern recognition that characterized nervous systems for so long. It gets even worse: what if we want to discriminate between approaching footfalls (each footfall is louder than the previous one) and departing footfalls (each footfall is weaker than the previous one)? That requires us to add a new circuit for remember not just whether or not there was a footfall, but for how loud it was -- that’s a much bigger circuit. And we also must add more circuitry to compare the loudness of one footfall with the loudness of another footfall -- that’s really complicated!
My point here is that all this sequential processing is horrendously complicated and requires oodles of neurons. If we’re just recognizing patterns, we can do that with a small brain using a few neurons. But if we want to recognize events that are stretched out over time -- what I call sequential events -- then we’re going to need a larger brain to do even simple sequential processing.
An analogy from electronics
Interestingly enough, there’s a parallel problem in electronics. If you want to built a simple pattern recognizing circuit, it takes just a handful of simple circuits called gates. A circuit to recognize an eight-bit pattern might look like this:
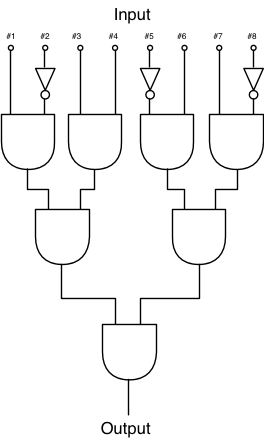
This little circuit will trigger when it gets the pattern 10110110, which is equal to the number 182, as an input. However, should you wish to transmit this number using a standard serial protocol such as RS-232, then your circuitry becomes vastly more complicated:
Mind you, this is not an actual circuit diagram like the one above; this is a block diagram showing only blocks, each of which represents large circuits containing many gates, shift registers, and other components. The point is that serial processing demands much more complexity than parallel processing.
Serial processing in animals
Sometime during the Triassic, animals started developing the capability for serial processing. It’s impossible to know much about the history, but we know that mammals, which had their origins in the Triassic, all possess some capability for serial processing, whereas reptiles and amphibians don’t. Birds, which got their start somewhat later, show mixed abilities for serial processing. In general, they’re pretty bad at it, but in certain specifics their serial processing capabilities are excellent. The dinosaurs themselves never bothered to pick up on the advantages of serial processing. When you’re ten times bigger than a 500-pound gorilla, you don’t need no stinkin’ geek-mammal tricks.
Here’s a simple, utterly unscientific test for serial processing capabilities. Place a test animal inside a pen. Then open a gate in the pen, making certain that the animal is aware of the gate, but don’t allow the animal to escape just yet. Go to the opposite side of the pen and entice the animal with a delectable treat, where you prominently place the treat on the outside of the pen -- opposite the gate. Question: how long will it take the animal to figure out how to get the treat? The problem requires serial reasoning; the animal must figure out the path -- the sequence of steps -- necessary to reach the treat.
If it’s one of the smarter mammals, such as a dog, cat, or pig, it will figure out the solution almost immediately. An herbivore, such as a goat, cow, or horse, will take a little longer. A duck, chicken, turkey, or emu will never figure it out.
Another example of sequential reasoning is the evasion path taken by prey attempting to escape from a predator. Most mammals will zig and zag as they run, trying to throw the predator off balance, and they will take terrain factors into consideration as they run. Birds don’t know this trick; they flee directly away from the predator. In practical terms, this means that ducks and chickens are easy to herd, but goats or pigs require more cunning and some fast moves. I know.
Of course, those bigger brains didn’t come cheaply; on the contrary, brain matter is the most expensive kind of tissue an animal can have. One pound of brains gobbles up more nutrition than a pound of muscle, kidney, or skin. So animals with bigger brains must eat more food. The Darwinian question is, do the performance improvements offered by bigger brains justify all that extra food that must be eaten? Eventually, the mammals figured out how to answer that question in the affirmative.
Our next exciting episode:
Mammals invent learning via play
