Let’s go back to the tree mentioned earlier as an example of both Object and Process, looking more closely at the Processes at work:
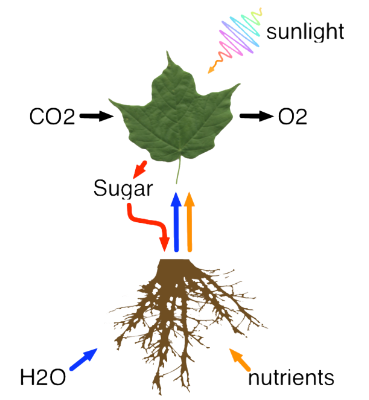
In this simple representation of the system of Processes at work in the tree, there are just five component Processes:
1. Minerals and nutrients in the soil dissolve into the water in the soil.
2. The water is absorbed in the roots.
3. The nutrient-laden water flows up into the leaves.
4. A complex chemical reaction in the cells of the leaf uses sunlight to convert carbon dioxide, water, and nutrients into sugars, releasing oxygen as a result.
5. The sugars fuel the growth of the tree.
This is a crude overview of the system. We could make it much more detailed; indeed, we could break it down into thousands of tiny processes. For example, let’s zoom in on the actual photosynthetic process:
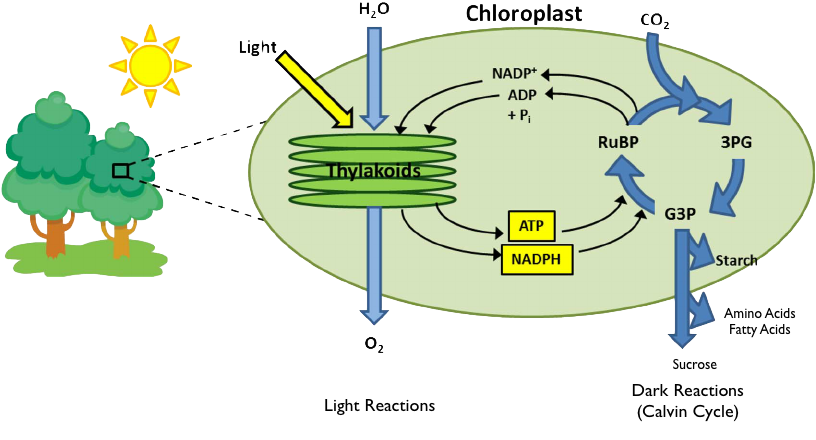
Again, we could zoom in on the details of these chemical Processes to break them down into even smaller Processes. The system of Processes is not infinitely large; at some point, we would have a complete diagram of every single Process at work — but it would be a very large diagram!
But there’s a more important problem with this diagram: it’s vague. If you wanted to use the computer to represent this system of Processes, you’d get nowhere, because this diagram doesn’t tell you anything about the Processes that you can express with the computer. It’s just a bunch of arrows. Have you ever tried to write a program with arrows? Sure, you can draw pretty diagrams of the system of Processes, but that’s about all. You can’t actually make Processes inside the computer that echo the Processes inside the tree. If you want to use the computer, you’re going to have to resort to the language of Process:

Oh no!
Fear of mathematics
Here you must confront head-on the most serious bias you face in attempting to design for the computer: your fear of mathematics. Your fears are well-nigh universal: EVERYBODY hates math. Well, yes, there are a few people who just love math, but there are also some people who like to smear feces on their faces. Most people don’t like smearing feces on their faces, and most people don’t like math, so let’s be honest: math sucks. Math stinks. Math is hateful. But math is the language of process, and it is the language you must use to express process on a computer. If you want to express yourself with a computer, you’ll have to learn to use math.

Do I really have to learn math?
Yes, you do. I’m sorry. It’s not my fault; it is intrinsic to the nature of the medium. But if you truly do have the soul of an artist, if your heart burns with the need to communicate the beauty you see to others, then you will gird your loins, put your shoulder to the wheel, and look algebra in the face.
I can offer you some small consolation: we’re not talking about this kind of math:
Instead, if you can speak high school math — algebra — you’ve got enough to put you way ahead of most software designers. But few people can handle high school algebra as adults. As they do with any traumatic event, they purge it from their memories. Even programmers suffer from this weakness. They can all handle boolean logic: fiddling around with AND, OR, EOR, IF, and so forth. That’s about as far as most programmers go with mathematics.
So go on a long walk and think about your purpose in life. You must weigh your revulsion of algebra against your need for artistic expression. It’s a lot easier to walk the well-trodden path of conventional forms of artistic expression: imagery, sound, animation, and language. You have thousands of great classics in each of these fields to show you the way. Artistic expression on the computer, on the other hand, is shrouded in darkness. Very little work has been done in using the computer as a medium of expression (as opposed to a tool for other media of expression). There are no classics to guide you. If this darkness is too scary, then don’t waste your time trying to use the computer as a medium of expression, and stop taking this course. On the other hand, if you have a soul that is intrigued and excited by darkness, if you are willing to face the ugliness and drudgery of this journey, then follow my voice coming from inside the dark and forbidding cave of mathematics.
If you are still with me, then you have made the committment to learn how to use algebra to express yourself. Good for you! Let me start by walking you through a simple example of how to do this. Later, we’ll get into something more artistically interesting. Let’s see how to use algebra to express the processes in tree growth, but I’ll use an even simpler system of Processes:
1. Water is absorbed in the roots and flows up into the leaves.
2. A complex chemical reaction in the cells of the leaf uses sunlight to convert carbon dioxide, water, and nutrients into sugars, releasing oxygen as a result.
3. The sugars fuel the growth of the tree.
Let’s work on each of these steps separately.
1. Water is absorbed in the roots and flows up into the leaves.
The critical idea here is that water is needed for the tree to grow. The amount of water available to the tree comes from the water content of the soil, so we need an algebraic variable for the water content of the soil. Let’s call it SoilWater and use a number between 0.0 and 1.0 to measure it. So if the tree is sitting in the middle of a lake, SoilWater is equal to 1.0. If the tree is in sand in the middle of the Sahara Desert, then SoilWater is 0.0. Of course, the amount of water that the tree takes up is less than the amount of water in the soil; the roots take up only some fraction of the water. Let’s call that the RootEfficiency of the tree, and it is another number between 0.0 and 1.0. If the roots are perfectly efficient, then they take up all available water, and the RootEfficiency is 1.0. If the roots are perfectly INefficient, then the RootEfficiency is 0.0.
So how much water does the tree get? Simple: it’s the amount of water available in the soil multiplied by the efficiency with which the roots take up the water. We create a new algebraic variable, AvailableWater, and write a simple equation for it:
AvailableWater = SoilWater * RootEfficiency
2. A complex chemical reaction in the cells of the leaf uses sunlight to convert carbon dioxide, water, and nutrients into sugars, releasing oxygen as a result.
This one is complicated because it uses three inputs: sunlight, carbon dioxide, and water. However, let’s simplify it by taking advantage of the fact that the amount of carbon dioxide in the atmosphere is constant at 400 parts per million (Yes, human emissions of CO2 are increasing that value, but we’re trying to keep things simple for now.) Since carbon dioxide is constant, we don’t need to include it in our formula; it doesn’t change, so it can’t change anything. So now we have only two input variables: AvailableWater and Sunlight. Obviously, more water makes it easier to synthesize more sugar molecules, and more sunlight has the same effect. So they amplify each other, which means that we multiply them together to get this formula:
SugarProduction = AvailableWater * Sunlight
You might wonder, “How did I know to multiply the two numbers together?” This is one of the easiest tricks in algebra, yet few people understand it. When you want to combine two variables, your most obvious choice is between addition and multiplication.
(Subtraction is just backwards addition, and division is just backwards multiplication, so you really don’t need to consider them separately. For this decision, you need only decide whether the effect of a variable is positive or negative — does it increase or decrease the result?)
Just one question makes the choice for you: Are both variables necessary, or can either one alone produce the output? To put it another way, if either one of the variables is zero, and the result must therefore be zero, then you must multiply them together. But if one or the other can do the job, then you add them. To put it even more simply, if you must have BOTH one variable AND the other, then multiply. If you can have EITHER one variable OR the other, then you add them.
In this case, the tree must have water, and it must have sunlight. All the water in the world with zero sunlight doesn’t cut the mustard; neither does all the sunlight in the world with zero water. Therefore, we multiply them together.
3. The sugars fuel the growth of the tree.
This is easy: the more sugar, the faster the tree grows. So we get a simple equation:
TreeGrowth = SugarProduction
This is a very simple example of how we can use mathematics to represent the processes by which a tree grows. It boils down to a simple question: how much water is there, and how much sunlight is there? We could of course make it much more complicated, including all sorts of interesting factors. But this is what we call a “first approximation”; it’s a good start on the problem. I won’t go into the process of making it more complete; you should digest the simple concepts in this lesson before proceeding to the more complex issues in subsequent lessons.
Here’s another essay I wrote on the significance of mathematics.
